Передаточная функция САУ

Передаточной функцией системы называют отношение изображения Лапласа для выходной и входной величин при их начальных нулевых условиях и при отсутствии других воздействий. Она полностью определяет динамические свойства системы и представляет собой комплексное выражение (2.17)

.

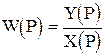Системы автоматического регулирования являются замкнутыми системами. Но при их анализе часто рассматривается разомкнутая цепь звеньев, которая затем замыкается. Составим сначала передаточные функции разомкнутой цепи звеньев.

1.5.1. Последовательное соединение звеньев(рис.1.5.1)

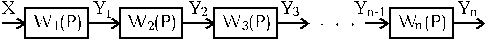
Рис.1.5.1. Последовательное соединение звеньев

Пусть заданы передаточные функции всех звеньев

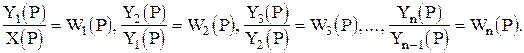(1.5.1)

Если перемножить все левые части и все правые части этих равенств, получим искомый результат

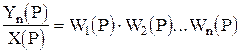
или (1.5.2)

т.е. передаточная функция разомкнутой цепи последовательно соединенных звеньев равна произведению передаточных функций всех звеньев.

1.5.2. Параллельное соединение звеньев (рис.1.5.2,а)

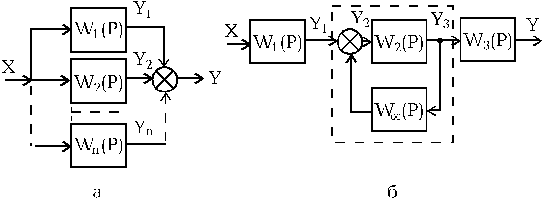
Рис.1.5.2. Параллельное (а) и встречно-параллельное (б)
соединение звеньев

Пусть заданы передаточные функции звеньев

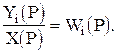
Так как выходная величина цепи равна

,

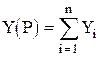то передаточная функция цепи получит вид

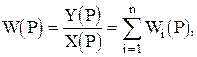(1.5.3)

т.е. передаточная функция разомкнутой цепи из параллельно соединенных звеньев равна сумме передаточных функций всех звеньев.

1.5.3. Встречно-параллельное соединение звеньев (рис.1.5.2,б)

В таком соединении образуется замкнутый контур прохождения сигнала и создается эффект обратной связи.

Согласно схеме, обведенной пунктиром, имеем в изображениях по Лапласу

Y₂(P)=Y₁(P)-Y_oc(P), Y_oc(P)=W_oc(P)×Y₃(P). (1.5.4)

Но далее

Y₃(P)=W₂(P)×Y₂(P)=W₂(P)(Y₁(P)-W_oc(P)Y₃(P)). (1.5.5)

Отсюда получаем

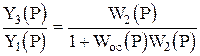. (1.5.6)

Найдем передаточную функцию цепи с остальными звеньями путем перемножения выражения (1.5.6) с передаточными функциями последовательных звеньев:

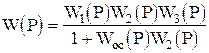. (1.5.7)

На основании выражений (1.5.1)...(1.5.7) можно получить передаточные функции любых соединений звеньев (рис.1.5.3).

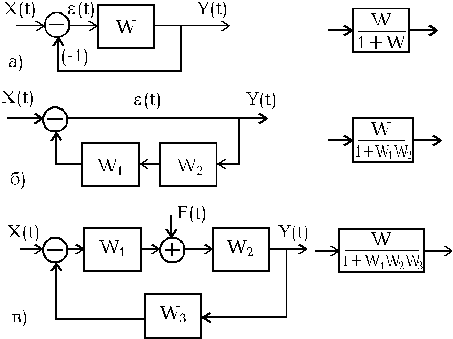
Рис.1.5.3. Эквивалентные преобразования структурных
схем САУ