Дифференцирующие звенья

Дифференцирующие звенья реагируют на скорость изменения входного воздействия. Рассмотрим идеальное (безынерционное), реальное (инерционное и форсирующее звенья).

1. Идеальное (безынерционное) дифференцирующее звено описывается уравнением и передаточной функцией

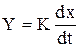, W(P)=KP. (1.4.11)

Частотные характеристики звена имеют вид (рис.1.4.5):

W(jw) = jKw, A(w) =Kw, j = +90°,

L(w) = 20 lgK + 20 lgw, h(t) = Kd(t), . (1.4.12)

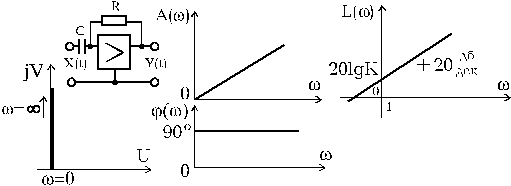
Рис. 1.4.5. Частотные характеристики идеального
дифференцирующего звена

Примерами идеального дифференцирующего звена может служить тахогенератор и RC цепочка с усилителем.

2. Реальное (инерционное) дифференцирующее звено описывается уравнением и передается функцией

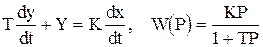, (1.4.13)

т.е. является последовательным соединением двух простых звеньев - идеального дифференцирующего с передаточной функцией K₁P и апериодического с передаточной функцией K₂/(1+TР), где K₁K₂=K.

Частотные характеристики звена имеют вид (рис.1.4.6):

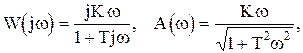j=90°- arctgTw,

,

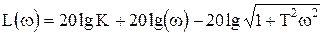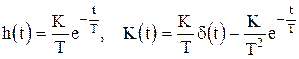. (1.4.14)

Рис. 1.4.6. Частотные характеристики реального
(инерционного) дифференцирующего звена

3. Форсирующее звено является реальным дифференцирующим звеном, получаемым при параллельном соединении пропорционального и дифференцирующего звеньев, с уравнением и передаточной функцией:

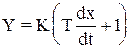, W(P)=K(TР+1) (1.4.15)

Частотные характеристики звена имеют вид (рис.1.4.7):

W(jw)=K(1+jTw), , j=arctgTw,

,

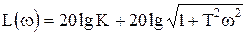h(t)=K(1+Td(t)), 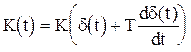. (1.4.16)

Рис. 1.4.7. Частотные характеристики форсирующего
звена