Логарифмические частотные характеристики

Так как при построении АФЧХ, АЧХ и ФЧХ частота и амплитуда изменяются в очень больших пределах, то с использованием процедуры логарифмирования можно значительно уменьшить изображения этих характеристик.

При построении логарифмической амплитудно-частотной характеристики (ЛАЧХ) по оси ординат откладывают величину

20lgA(w) = 20lg½W(jw)½= L(w), (1.3.21)

единицей измерения для которой является децибел.

По оси абсцисс откладывается частота w в логарифмическом масштабе (рис.1.3.6).

Равномерной единицей на оси абсцисс является декада - любой отрезок, на котором значение частоты увеличивается в 10 раз. Точка пересечения ЛАЧХ с осью абсцисс называется частотой среза w_c.

Начало координат помещают в точке w=1, так как lg1=0. При L=0 A=1, т.е. система пропускает сигнал в натуральную величину. При L>0 происходит усиление, а при L<0 - ослабление амплитуды.

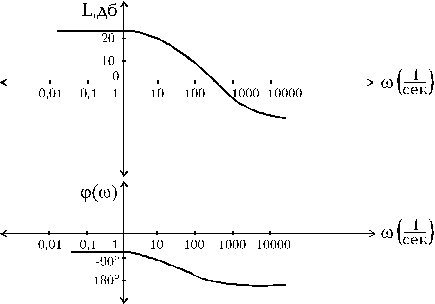
Рис.1.3.6. Логарифмические амплитудно-частотные и
фазо-частотные характеристики

Типовые звенья САУ

Современные САУ состоят из элементов (звеньев), разнообразных по конструкции, материалам и виду использованной энергии элементов, выполняющих различные функции.

Типы звеньев САУ различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики.

Основные типы звеньев делятся на 3 группы: позиционные, дифференцирующие и интегрирующие.

Позиционные звенья

Позиционными звеньями называются такие, в передаточной функции которых

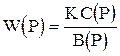(1.4.1)

многочлены В(Р) и С(Р) имеют свободные члены (равные I), т.е. эти звенья обладают статической характеристикой Y=KX при P=0, определяющей их состояние равновесия (свойство позиционности).

1. Идеальное усилительное звено в статике и в динамике описывается алгебраическим уравнением, а передаточная функция его является коэффициентом усиления (передачи):

Y(t)=KX(t); W(P)=K. (1.4.2)

Амплитудно-фазовая, амплитудно-частотная, фазо-частотная и логарифмическая амплитудно-частотные характеристики приведены на рис.1.4.1 и представляют собой следующие выражения:

W(jw)=K, A(w)=K, j(w)=0. (1.4.3)

Переходная и весовая функции:

h(t)=K (t>0), K(t)=K₁d(t). (1.4.4)

Рис.1.4.1. Частотные характеристики идеального звена

Примерами идеального звена могут быть большинство датчиков, делители напряжения, широкополосный электронный усилитель, механический редуктор.

2. Апериодическое (инерционное) звено описывается уравнением и передаточной функцией

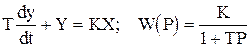. (1.4.5)

Частотные функции звена имеют вид (рис.1.4.2)

j(w)=arctgTw, W(jw)=U(w)+jV(w),

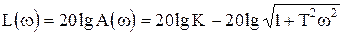. (1.4.6)

Переходная функция, согласно решению уравнения звена, при X=1(t) и нулевых начальных условиях имеет вид

,

а весовая функция

.

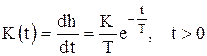Рис.1.4.2. Частотные характеристики апериодического звена

Примерами апериодического звена являются электродвигатель, термопара и LR цепь.

3. Апериодическое звено 2-го порядка описывается дифференциальным уравнением и передаточной функцией:

, (1.4.7)

т.е. апериодическое звено 2-го порядка эквивалентно последовательному включению двух простых апериодических звеньев, у которых K₁K₂=K.

Частотные свойства звена имеют вид (рис.1.4.3):

,

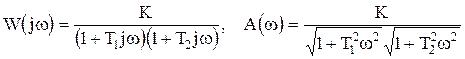j(w)=-arctgT₁w-arctgT₂w,

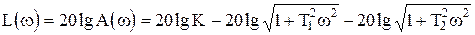, (1.4.8)

,

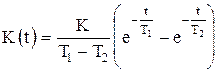, t>0.

Примерами могут служить: двойная LR цепочка, электромашинный усилитель, двигатель постоянного тока с электрической цепью статора и якоря.

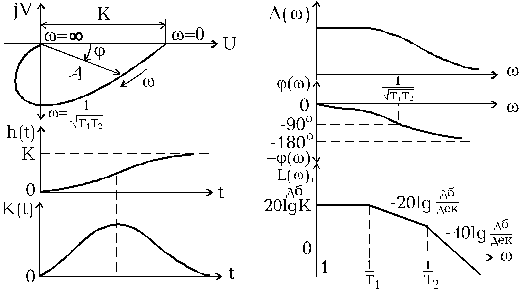
Рис.1.4.3. Частотные характеристики апериодического
звена 2-го порядка

4. Колебательное звено имеет математическое описание, близкое к описанию апериодического звена при T₁=T₂:

, (1.4.9)

где а - коэффициент демпфирования колебаний (затухания), 0<a<1 и чем больше а, тем быстрее затухают колебания.

Частотные характеристики звена имеют вид (рис.1.4.4):

,

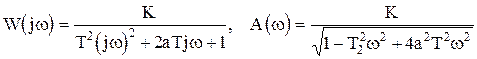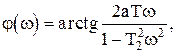
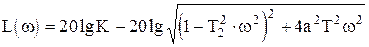, (1.4.10)

,

.

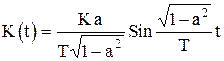
Рис.1.4.4. Частотные характеристики колебательного звена

Примерами колебательных звеньев могут быть: последовательное или параллельное соединение LCR цепочек (звеньев), гидродинамический усилитель, электрический контур резонансного стабилизатора.

Частный случай колебательного звена при a=0, когда h(t) и K(t) становятся незатухающими (периодическими), носит название консервативного звена.

Коэффициент а в математике, в радиотехнике и теории автоматического управления называют декрементом затухания.

В результате исследований доказано, что оптимальные переходные режимы достигаются при a » 0,7. В этом случае перерегулирование составляет около 4,3% (критерий по ограничению задается 5%), время переходного процесса не превышает 2pT, т.е.

t_пп » 4,7aT.

При этих значениях обеспечивается технический оптимум или оптимальный модуль.

При а=0,5 перерегулирование превышает 30%, длительность увеличивается в 2 раза. При a ³1 длительность переходного процесса в 3-4 раза больше.