Критерий устойчивости Гурвица
Алгебраический критерий устойчивости работает только на САУ 1 и 2-го порядка.
Для САУ более высокого порядка применяется критерий устойчивости Гурвица.
Для устойчивости системы необходимо и достаточно, чтобы были положительными главные определители Гурвица, составленные из квадратной матрицы коэффициентов характеристического уравнения.
Правило составления определителей Гурвица следующее:
1. По диагонали матрицы от левого верхнего угла до правого нижнего угла записываются все коэффициенты характеристического уравнения САУ от a1 до an.
2. Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента, а также если индекс его меньше нуля или больше n, на месте его пишется нуль.
3. Из матрицы выбираются диагональные миноры и они являются определителями Гурвица.
| a1 | a3 | a5 | . | . . | ||||
| a0 | a2 | a4 | . | . . | ||||
| a1 | a3 | . | . . | |||||
| a0 | a2 | . | . . | . (1.6.13) | ||||
| . . | . . | . . | . | . . | . | . | ||
| . | . . | an-1 | ||||||
| . | . . | an-2 | an |
Указанные определители Гурвица имеют вид:
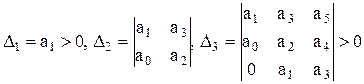 ... (1.6.14)
... (1.6.14)
Пример. Рассмотрим устойчивость замкнутой системы (1.5.5) с передаточной функцией разомкнутой системы (рис.1.6.3).
 .
.
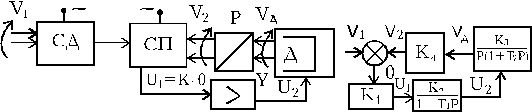
Рис.1.6.3. Система дистанционного слежения:
СД - сельсин-датчик; СП - сельсин-приемник;
Р - редуктор; Д - двигатель; У - усилитель
Характеристическое уравнение замкнутой системы имеет третий порядок
1+W(P)=0, T1T2P3+(T1+T2)P2+P+K=a0P3+a1P2+a2P+a3=0. (1.6.15)
Определитель Гурвица будет иметь вид:
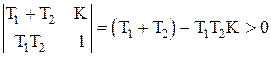 (1.6.16)
(1.6.16)
или
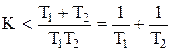 . (1.6.17)
. (1.6.17)
Для K=80, T1=0,12c, T2=0,05c условие (1.6.17) не выполняется - система неустойчива. Для данных T1 и T2 система устойчива при K=Kкр=28.
Дата добавления: 2021-12-14; просмотров: 495;











