Интегрирующие звенья

В интегрирующих звеньях выходная величина пропорциональна интегралу по времени от входной величины. В отличие от позиционных звеньев интегрирующие звенья не приходят к установившемуся новому состоянию, а их выходная величина имеет тенденцию к неограниченному увеличению.

1. Идеальное интегрирующее звено характеризуется пропорциональностью между входной величиной и скоростью изменения выходной величины. Описывается уравнением, передаточной функцией и частотными характеристиками (рис.1.4.8):

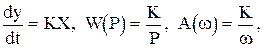j(w) = -90°,

L(w) = 20 lgK - 20 lgw, (1.4.17)

h(t)=Kt×1(t), K(t)=K×1(t).

2. Реальное (инерционное) интегрирующее звено описывается уравнением и передаточной функцией

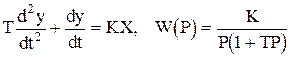. (1.4.18)

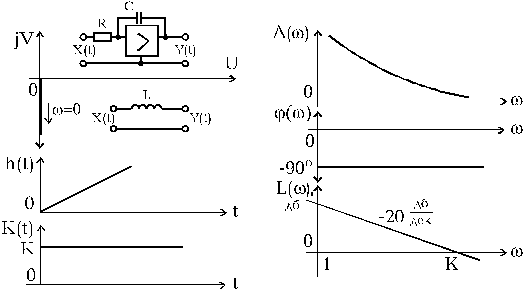
Рис. 1.4.8. Частотные характеристики идеального
интегрирующего звена

По существу оно является последовательным соединением двух простых звеньев - идеального интегрирующего 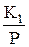и апериодического K₂(1+TР)^-1.

Частотные характеристики звена имеют вид (рис. 1.4.9):

, j(w)=-90-arctgTw,

,

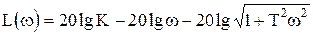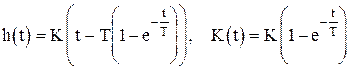. (1.4.19)

3. Изодромное звено описывается уравнением и передаточной функцией

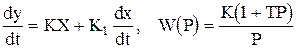, (1.4.20)

где T=K₁/K₂ - постоянная времени.

Из передаточной функции следует, что звено это состоит из последовательного соединения идеально интегрирующего K₁/P и форсирующего K₂(1+TP) звеньев K₁K₂=K.

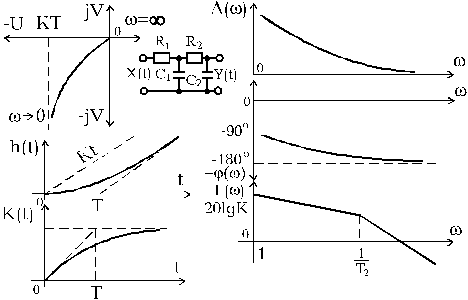
Рис. 1.4.9. Частотные характеристики реального
интегрирующего звена

Частотные характеристики имеют вид (рис.1.4.10):

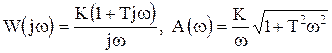, j(w)=-90+arctgTw,

,

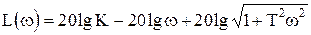h(t)=Kt+K₁, K(t)=K+K₁d(t). (1.4.21)

Рис.1.4.10. Частотные характеристики изодромного
звена