Понятие об устойчивости и виды устойчивости

Основным динамическим свойством САУ является ее устойчивость. Устойчивостью называется свойство системы возвращаться в исходное или новое установившееся состояние после всякого выхода из него в результате внешнего воздействия (рис.1.6.1). Неустойчивые системы разрушаются, они неработоспособны. Поэтому актуальнейшей инженерной задачей является проверка САУ на устойчивость и обеспечение ее устойчивости.

Устойчивость системы необходимо исследовать в следующих случаях: при определении структуры САУ, при выборе параметров звеньев, при настройке и выборе допустимых пределов изменения параметров.

Устойчивость линейной системы не зависит от величины возмущения. Доказано Ляпуновым, что линейная динамическая системы, устойчивая при малых возмущениях, будет устойчивой и при больших возмущениях. Поэтому для суждения об устойчивости САУ достаточно определить устойчивость в "целом" по передаточной функции системы. Так как передаточная функция представляется в виде (1.2.8) и (1.2.17):

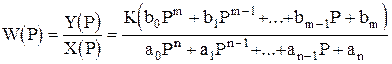, (1.6.1)

где К - коэффициент; a₀, a₁,... a_n - коэффициенты полинома выходного параметра; b₀, b₁,... b_n - коэффициенты полинома входного воздействия; - оператор дифференцирования.

Отсюда видно, что математическая модель САУ представляется в виде параметрического и дифференциального уравнений:

(a₀Pⁿ+ a₁P^n-1+...+a_n-1P+a_n)Y(t)=(b₀P^m+b₁P^m-1+...+b_m-1P+b_m)X(t) (1.6.2)

или

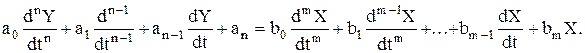(1.6.3)

Мы уже ознакомились с решением дифференциальных уравнений (1.2.8)...(1.2.11), т.е. Y(t)=Y_вын.+Y_св(t),

где Y_вын. - частное решение уравнения, определяющее вынужденное движение для производных равных нулю;

Y_св(t) - решение левой части уравнения, приравненное нулю (свободная составляющая).

Считают, что САУ устойчива, если свободная составляющая будет затухать, т.е.

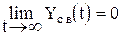. (1.6.4)

Свободная составляющая представляется в решении уравнения (1.6.3) следующим видом:

, (1.6.5)

где l_i - корни характеристического уравнения, полученного из левой части уравнения (1.6.2) или (1.6.3):

a₀lⁿ+a₁l^n-1+...+a_n-1l+a_n=0. (1.6.6)

Решение характеристического уравнения зависит от его корней, которые в общем виде могут быть комплексными

l_i = ± a_i ± jb_i. (1.6.7)

Рассмотрим лишь две составляющие процесса от пары сопряженных комплексных корней

Y_св(t)=c_ie^(ai+jbi)t+c_i+1e^(ai-jbi)t= , (1.6.8)

где c_i, c_i+1, - постоянные коэффициенты;

b_i - частота колебаний;

a_i - коэффициент затухания;

j_i - фаза колебаний.

Анализ (1.6.8) показывает, что это синусоида с амплитудой, изменяющейся по экспоненте . Поэтому, если:

1) a_i<0, e^aitуменьшается при t®¥, колебание затухает и САУ устойчива (рис.1.6.1,а,б);

2) a_i>0, e^aitувеличивается при t®¥, колебание увеличивается и САУ неустойчивая (рис.1.6.1,д);

3) a_i=0 - незатухающие колебания и САУ на границе устойчивости (рис.1.6.1,а);

4) b_i=0 - процесс апериодический (рис.1.6.1,в).

Результаты анализа и виды устойчивости показаны на рис.1.6.1.

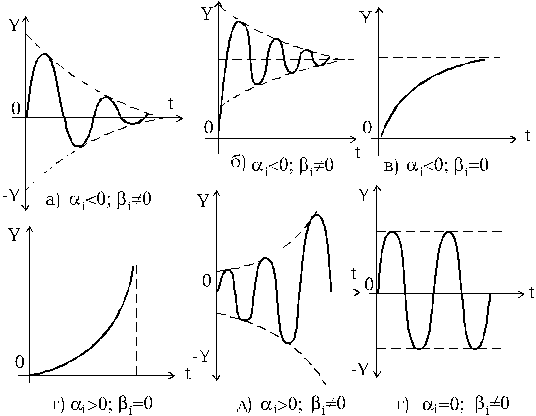
Рис.1.6.1. Переходные процессы устойчивых (а,б,в)
и неустойчивых (г,д) САУ