Уравнение Ферма-Пелля
Так называется диофантово уравнение x2 – A×y2 = 1, где A Î N. Его исследование было начато П. Ферма, а окончательное описание решений получено Л. Дирихле. Дж. Пелль не имеет к решению этого уравнения никакого отношения, его имя ошибочно связал с этим уравнением Л. Эйлер.
 I. Рациональные решения.Вначале найдём все рациональные решения уравнения Ферма-Пелля.
I. Рациональные решения.Вначале найдём все рациональные решения уравнения Ферма-Пелля.
Кривая g с уравнением Ферма x2 – A×y2 = 1 имеет канонический вид 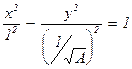 и, как известно, является гиперболой с вершинами (±1; 0) и асимптотами y = ±
и, как известно, является гиперболой с вершинами (±1; 0) и асимптотами y = ± 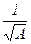 ×x .
×x .
Выберем на ней рациональную точку – её вершину S(1; 0), с помощью которой проведём параметризацию остальных рациональных точек этой кривой.
Если точка M(r ; s) Î g рациональна, т.е. r, s Î Q, то прямая (MS) имеет каноническое уравнение 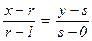 Û y =
Û y = 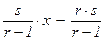 и угловой коэффициент k =
и угловой коэффициент k = 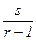 Î Q .
Î Q .
Обратно, если заданугловой коэффициент k Î Q , то можно найти все точки пересечения прямой y = k×(x – 1), проходящей через точку S, с кривой x2 – A×y2 = 1 : одна из них S, а вторая находится из соотношений
x2 – A×k2×(x – 1)2 = 1 Û (x – 1)×(x + 1) = A×k2×(x – 1)2 Û
Û (1 – A×k2)×x = –1 – A×k2 Û 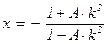 .
.
Знаменатель последнего выражения не обращается в ноль, если число A не является квадратом рационального числа: 1 – A×k2 = 0 Û A = 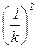 . В случае натурального параметра A это возможно только если A полным квадратом. Действительно, если
. В случае натурального параметра A это возможно только если A полным квадратом. Действительно, если 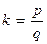 – несократимая дробь, то A =
– несократимая дробь, то A = 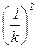 Û Û A×p2 = q2 и т.к. p и q взаимно просты, то A = m×q, m×p2 = q, а значит, m = q×s, s×p2 = 1 и s = 1, p = ±1, а A = q2.
Û Û A×p2 = q2 и т.к. p и q взаимно просты, то A = m×q, m×p2 = q, а значит, m = q×s, s×p2 = 1 и s = 1, p = ±1, а A = q2.
Теорема (о рациональных решениях уравнения Ферма-Пелля). Все рациональные точки кривой x2 – A×y2 = 1 (A Î N) имеют вид M(x ; y), где
· 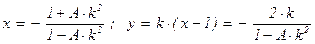 (k Î Q), если A не является полным квадратом;
(k Î Q), если A не является полным квадратом;
· 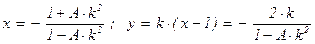 (k Î Q \ {
(k Î Q \ { 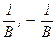 }), если A = B2 ;
}), если A = B2 ;
II. Целочисленные решения.Теперь рассмотрим целочисленные решения уравнения Ферма. Прежде всего, заметим, что имеет смысл рассматривать только уравнения, в которых A не является полным квадратом: если A = B2, то
x2 – A×y2 = 1 Û x2 – B2×y2 = 1 Û (x + B×y)×(x – B×y) = 1 Û
Û 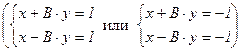 Û
Û 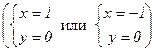 .
.
Такие решения назовём тривиальными.
1. Арифметика чисел x + 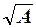 ×y (x, y Î Z). Левая часть уравнения Ферма-Пелля разложима на множители: x2 – A×y2 = (x +
×y (x, y Î Z). Левая часть уравнения Ферма-Пелля разложима на множители: x2 – A×y2 = (x +  ×y)×(x –
×y)×(x –  ×y). Поэтому числа вида x +
×y). Поэтому числа вида x +  ×y, где x, y Î Z , играют важную роль в исследовании решений этого уравнения. Обозначим
×y, где x, y Î Z , играют важную роль в исследовании решений этого уравнения. Обозначим
K = {x +  ×y Î R | x, y Î Z}.
×y Î R | x, y Î Z}.
В дальнейшем будем отождествлять решение (x; y) этого диофантова уравнения с числом x +  ×y.
×y.
Для любого числа x +  ×y определим норму N(x +
×y определим норму N(x +  ×y) = x2 – A×y2.
×y) = x2 – A×y2.
Следующие формулы показывают, что множество рассматриваемых чисел замкнуто относительно сложения, вычитания, умножения, оно содержит 0 и 1, –1:
(x +  ×y) + (z +
×y) + (z +  ×t) = (x + z) +
×t) = (x + z) +  ×(y + t),
×(y + t),
(x +  ×y) – (z +
×y) – (z +  ×t) = (x – z) +
×t) = (x – z) +  ×(y – t),
×(y – t),
(x +  ×y)×(z +
×y)×(z +  ×t) = (x×z + A×y×t) +
×t) = (x×z + A×y×t) +  ×(x×t + y×z),
×(x×t + y×z),
0 = 0 +  ×0, 1 = 1 +
×0, 1 = 1 +  ×0, –1 = –1 +
×0, –1 = –1 +  ×0.
×0.
Для двух чисел x +  ×y, z +
×y, z +  ×t Î K можно вычислить их частное
×t Î K можно вычислить их частное
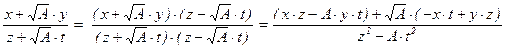 ,
,
которое не обязательно принадлежит K. Однако это частное принадлежит K, если x×z – A×y×t M z2 – A×t2 и –x×t + y×z M z2 – A×t2. Эти условия выполняются, например, в случае N(z +  ×t) = z2 – A×t2 = ±1.
×t) = z2 – A×t2 = ±1.
Для числа a = x +  ×y Î K определим
×y Î K определим 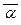 = x –
= x –  ×y Î K – сопряжённое число к a . Легко проверить следующие свойства сопряжённых чисел:
×y Î K – сопряжённое число к a . Легко проверить следующие свойства сопряжённых чисел:
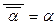 ,
, 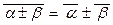 ,
,
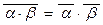 ,
,
N(±1) = 1, N(0) = 0.
Кроме того, норма от произведения чисел равно произведению норм:
N(a×b) = (a×b)× 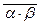 = (a×b)×(
= (a×b)×( 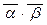 ) = a×
) = a× 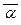 ×b×
×b× 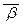 = N(a)×N(b).
= N(a)×N(b).
Ясно, что решения уравнения Ферма-Пелля имеют единичную норму. Значит, множество решений замкнуто относительно умножения и деления.
2. Приближение действительных чисел рациональными. Напомним лемму, доказанную ранее с помощью принципа Дирихле.
Лемма (о приближении действительных чисел рациональными). Для любого действительного числа r > 0 и произвольного n Î N найдутся такие натуральные числа a, b Î N, где 1 £ b £ n, что |b×r – a| £ 
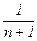 .
.
Будем использовать её для r =  .
.
3. Существование решения уравнения Ферма-Пелля. Докажем, что при любом A Î N диофантово уравнение x2 – A×y2 = 1 имеет нетривиальное решение, в котором y ¹ 0.
Зафиксируем произвольное n Î N и, пользуясь доказанной леммой, найдём an Î Z и 1 £ bn < n со свойством |an –  ×bn| <
×bn| <  . Тогда
. Тогда
|an2 – A×bn2| = |an –  ×bn|×|an +
×bn|×|an +  ×bn| <
×bn| <  ×|(an –
×|(an –  ×bn) + 2×
×bn) + 2×  ×bn| £
×bn| £
£  ×(|an –
×(|an –  ×bn| +2×|bn|×
×bn| +2×|bn|×  ) <
) <  ×(
×(  + 2×n×
+ 2×n×  ) = 2×
) = 2×  +
+ 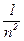 £ 2×
£ 2×  + 1.
+ 1.
Поэтому натуральная величина |an2 – A×bn2| принимает лишь конечное число значений на парах (an ; bn) при n Î N. Количество таких пар бесконечно, т.к. величина |an –  ×bn| <
×bn| <  стремится к нулю при n ® ¥ и не может быть равной нулю, поскольку
стремится к нулю при n ® ¥ и не может быть равной нулю, поскольку  иррационален. По принципу Дирихле получаем, что некоторое значение c величины |an2 – A×bn2| принимается бесконечное число раз. Пусть M = {(a; b) Î Z2 | |a2 – A×b2| = с} – бесконечное множество. Если c = 1, то всё доказано: при a2 – A×b2 = – 1 квадрат (a +
иррационален. По принципу Дирихле получаем, что некоторое значение c величины |an2 – A×bn2| принимается бесконечное число раз. Пусть M = {(a; b) Î Z2 | |a2 – A×b2| = с} – бесконечное множество. Если c = 1, то всё доказано: при a2 – A×b2 = – 1 квадрат (a +  ×b)2 = (a2 + A×b2) + 2×a×b×
×b)2 = (a2 + A×b2) + 2×a×b×  будет решением, т.к. N(a2) = N(a)2.
будет решением, т.к. N(a2) = N(a)2.
Поскольку множество M бесконечно, а множество остатков при делении на c конечно, то найдутся две такие различные пары (a1 ; b1), (a2 ; b2) Î M, что |a12 – A×b12| = c = |a22 – A×b22| и a1 º a2 , b1 º b2 (mod c). Для доказательства достаточно по принципу Дирихле раскладывать пары (a; b) Î M по кучам (r; s) – всем парам остатков от деления на c (0 £  £ c).
£ c).
Поскольку знаки чисел x, y в решении x + y×  можно менять произвольно, будем считать, что ai > 0, bi > 0 (i = 1, 2).
можно менять произвольно, будем считать, что ai > 0, bi > 0 (i = 1, 2).
Теперь получаем
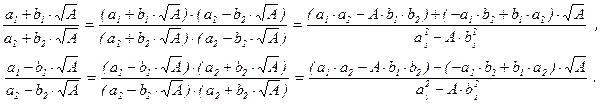
Поскольку a22 – A×b22 = c и a1 º a2 , b1 º b2 (mod c), то a1×a2 – A×b1×b2 º º a12 – A×b12 = c º 0, –a1×b2 + b1×a2 º –a1×b1 + b1×a1 = 0 (mod c).
Поэтому числа 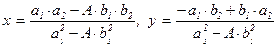 Î Z, причём
Î Z, причём
x2 – A×y2 = (x + y×  )×(x – y×
)×(x – y×  ) =
) = 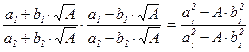 = ±1.
= ±1.
При этом y ¹ 0: если y = 0, то x = ±1 = x + y×  =
= 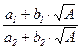 , т.е. вопреки выбору получаем (a1 ; b1) = (a2 ; b2).
, т.е. вопреки выбору получаем (a1 ; b1) = (a2 ; b2).
Найденное нетривиальное решение a = x + y×  порождает бесконечную серию решений a n (n Î Z), которые все различны как степени числа, не равного по модулю единице.
порождает бесконечную серию решений a n (n Î Z), которые все различны как степени числа, не равного по модулю единице.
Итак, доказана
Теорема (о существовании нетривиальных решений уравнения Ферма-Пелля). Уравнение Ферма-Пелля x2 – A×y2 = 1 имеет бесконечное количество нетривиальных решений.
4. Структура решений.Ясно, что если x + y×  – решение, то числа (–x) + y×
– решение, то числа (–x) + y×  , x + (–y)×
, x + (–y)×  , (–x) + (–y)×
, (–x) + (–y)×  тоже являются решениями. Поэтому с любым нетривиальным решением, у которого y ¹ 0, уравнение Ферма-Пелля имеет и положительное решение, у которого x > 0, y > 0. Положительное решение x0 + y0×
тоже являются решениями. Поэтому с любым нетривиальным решением, у которого y ¹ 0, уравнение Ферма-Пелля имеет и положительное решение, у которого x > 0, y > 0. Положительное решение x0 + y0×  с наименьшим значением x во множестве всех положительных решений назовём основным.
с наименьшим значением x во множестве всех положительных решений назовём основным.
На самом деле 1 +  < x0 + y0×
< x0 + y0×  £ x + y×
£ x + y×  для каждого положительного решения x + y×
для каждого положительного решения x + y×  . Действительно, неравенство 1+
. Действительно, неравенство 1+  < x0+y0×
< x0+y0×  очевидно. Второе неравенство следует из минимальности x0 и соотношений x2 – A×y2 = 1 = x02 – A×y02 : 0 £ x2 – x02 = A×(y2 – y02), т.е. y ³ y0 , x ³ x0 и потому x0 + y0×
очевидно. Второе неравенство следует из минимальности x0 и соотношений x2 – A×y2 = 1 = x02 – A×y02 : 0 £ x2 – x02 = A×(y2 – y02), т.е. y ³ y0 , x ³ x0 и потому x0 + y0×  £ x + y×
£ x + y×  . Итак, величина основного решения минимальна.
. Итак, величина основного решения минимальна.
Теорема (о структуре решений уравнения Ферма-Пелля). Любое решение уравнения Ферма-Пелля является с точностью до знака степенью (положительной или отрицательной) основного решения.
Доказательство. Во-первых, как уже отмечалось выше, множество решений замкнуто относительно умножения и деления. Поэтому, если x = x0 + y0×  – основное решение, то все его степени тоже x n (n Î Z) будут тоже решениями.
– основное решение, то все его степени тоже x n (n Î Z) будут тоже решениями.
Рассмотрим теперь степени x , x 2 , … , x n , … основного решения. Ясно, что x > 1 и поэтому x n ® ¥ при n ® ¥ . Если a = x + y×  – положительное решение (x, y > 0), не равное никакой степени x n (n Î N), то найдётся однозначно определённое n Î N со свойством x k < a < x k+1. Тогда получаем решение b =
– положительное решение (x, y > 0), не равное никакой степени x n (n Î N), то найдётся однозначно определённое n Î N со свойством x k < a < x k+1. Тогда получаем решение b = 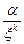 , причём 1 < b =
, причём 1 < b = 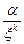 < x , что невозможно.
< x , что невозможно.
Итак, каждое положительное решение является степенью основного. Пусть теперь a = x + y×  – произвольное нетривиальное неположительное решение. Рассмотрим три возможных случая:
– произвольное нетривиальное неположительное решение. Рассмотрим три возможных случая:
1. x > 0, y < 0. Тогда 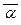 = x – y×
= x – y×  – положительное решение, так что
– положительное решение, так что 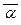 = x n и a =
= x n и a = 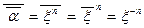 .
.
2. x < 0, y < 0. Тогда –a = (–x) + (–y)×  – положительное решение, и поэтому –a = x n , a = –x n .
– положительное решение, и поэтому –a = x n , a = –x n .
3. x < 0, y > 0. Тогда –a удовлетворяет случаю 1, так что –a = x –n и a = –x –n.
Теорема доказана.
Дата добавления: 2021-12-14; просмотров: 698;











