Ещё одно решение задачи о числе наборов

Цифр с заданной суммой компонент

Рассмотрим функцию 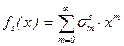, где для удобства считаем s₀^s = 0. Умножая приведённое выше рекуррентное соотношение на x^m+1 , получим

.

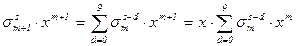Отсюда, суммируя по всем m ³ 1, находим

,

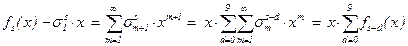т.е. 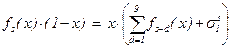, или .

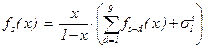Очевидно, что f_s-d(x) º 0 при s < d, f₀(x) = x + x² + … = 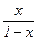, , 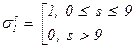f₁(x) = 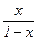×(f₀(x) + 1) = 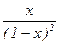. Поэтому при 1 £ k £ 8 имеемдва равенства:

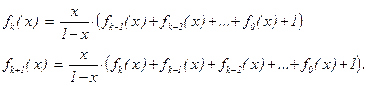
Вычитая из второго первое, получим f_k+1(x) – f_k(x) = 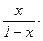f_k(x), т.е.

f_k+1(x) = 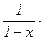f_k(x),

откуда f_k(x) = 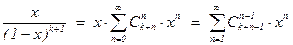при 0 £ k £ 9.

Далее,

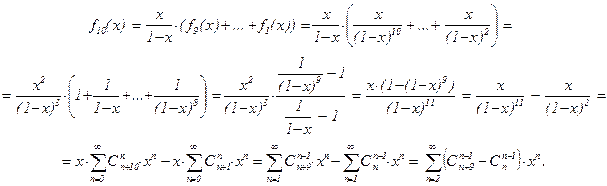
При k > 9 имеем

f_k(x) = 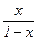×(f_k–1(x) + f_k–2(x) + … + f_k–8(x) + f_k–9(x)),

f_k+1(x) = 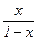×(f_k(x) + f_k–1(x) + … + f_k–7(x) + f_k–8(x)),

откуда после вычитания получаем f_k+1(x) – f_k(x) = 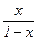×(f_k(x) – f_k–9(x)), т.е.

f_k+10(x) = 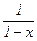×(f_k+9(x) – x×f_k(x)) (k = 0, 1, 2, …).

В частности, при k = 1 получим

f₁₁(x) = 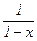×(f₁₀(x) – x×f₁(x)) =

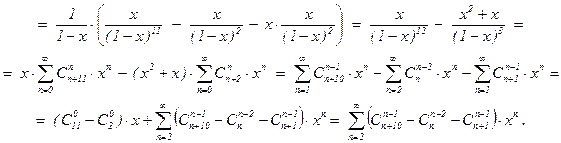
При k = 2:

f₁₂(x) = 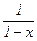×(f₁₁(x) – x×f₂(x)) =

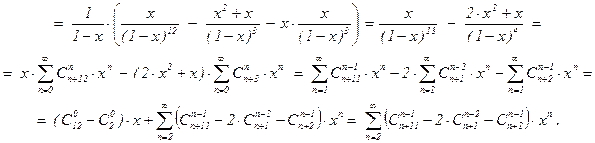
При k = 3:

f₁₃(x) = 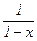×(f₁₂(x) – x×f₃(x)) =

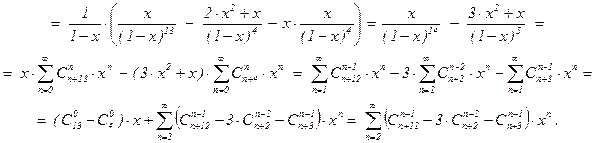
Ясно, что при 1 £ k £ 9 верны те же вычисления:

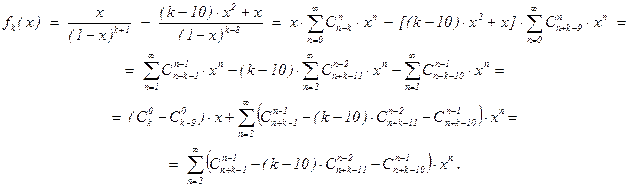Далее, f₂₀(x) = 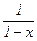×(f₁₉(x) – x×f₁₀(x)) =

= ,

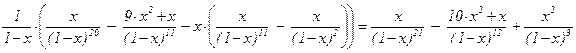f₂₁(x) = 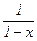×(f₂₀(x) – x×f₁₁(x)) =

= ,

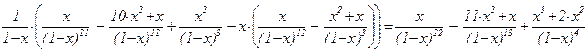f₂₂(x) = 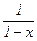×(f₂₁(x) – x×f₁₂(x)) =

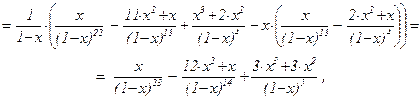
f₂₃(x) = 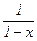×(f₂₂(x) – x×f₁₃(x)) =

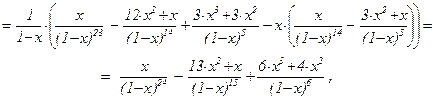
f₂₄(x) = 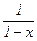×(f₂₃(x) – x×f₁₄(x)) =

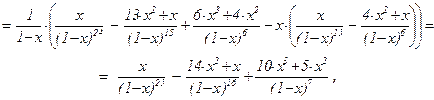
Если k = 10×2 + r (0 £ r £ 9), то

.

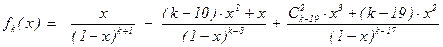В частности, .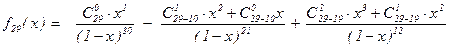

Далее, f₃₀(x) = 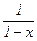×(f₂₉(x) – x×f₂₀(x)) =

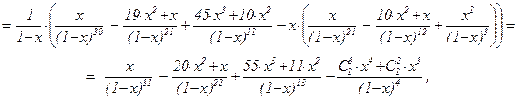
f₃₁(x) = 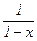×(f₃₀(x) – x×f₂₁(x)) =

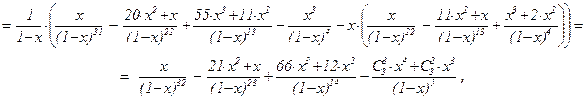
f₃₂(x) = 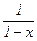×(f₃₁(x) – x×f₂₂(x)) =

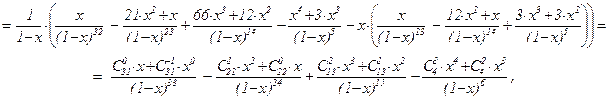
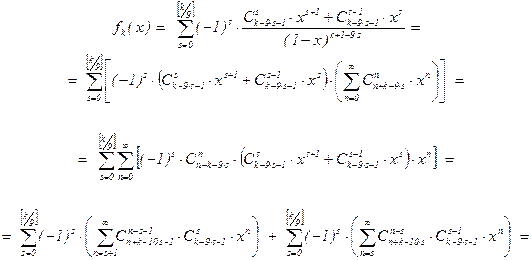
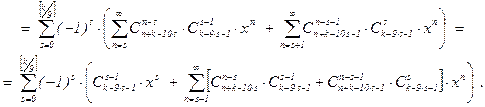
При этом

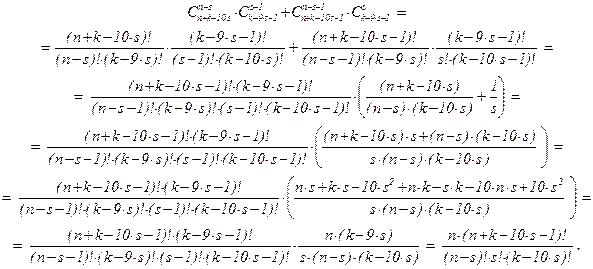
Таким образом,

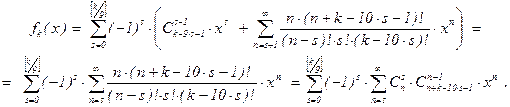
Итак,

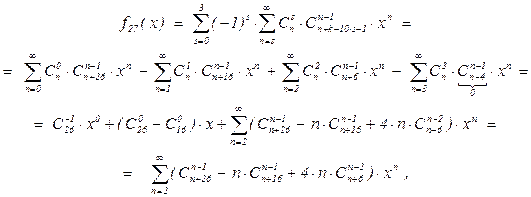
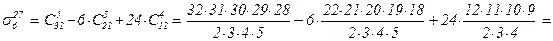
= 32×31×29×7 – 6×11×7×19×18 + 24×495 = 201376 – 158004 + 11880 = 55252.