Теоремы Эйлера и Ферма
Теорема (Эйлера).Для любого целого числа a, взаимно простого с натуральным модулем m, выполнено сравнение 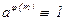 (mod m) .
(mod m) .
Доказательство. 1. Сведём задачу к числам 0 £ a < m. Для этого разделим a с остатком на m : a = m×q + r (0 £ r < m). При этом по свойству наибольшего общего делителя имеем
НОД(r, m) = НОД(a – m×q, m) = НОД(a, m) = 1,
т.е. r удовлетворяет условию теоремы. Если уже доказано, что rj(m) º 1 (mod m), то ввиду a º r (mod m) получим aj(m) º rj(m) º 1 (mod m).
Таким образом, можно предполагать, что 0 £ a < m.
2. Пусть M = {0, 1, 2, … , m – 1} и a1 , … , ak – все взаимно простые элементы множества M, из которых образуем множество M1 . По определению функции Эйлера k = j(m), а по условию теоремы имеем a Î M1 .
3. Рассмотрим элементы b1 = a×a1 , … , bk = a×ak . По свойствам взаимно простых чисел все эти элементы взаимно просты с m. Пусть r1 , … , rk – остатки от деления чисел b1 , … , bk на m : bi = m×qi + ri (0 £ ri < m, 1 £ i £ k). Тогда ri Î M (1 £ i £ k), и кроме того,
НОД(ri , m) = НОД(bi – m×qi , m) = НОД(bi , m) = 1,
так что ri Î M1 (1 £ i £ k).
4. Докажем, что среди чисел r1 , … , rk нет одинаковых. Действительно, если ri = rj , то bi = m×qi + ri , bj = m×qj + ri (0 £ ri < m). Тогда bi º ri º bj (mod m), т.е. a×ai º a×aj , a×(ai – aj) º 0 (mod m) и ввиду НОД(a, m) = 1 по свойствам сравнений верно ai – aj º 0, ai º aj (mod m), что значит ai = aj , что возможно только при i = j.
5. Итак, все числа r1 , … , rk различны, их число k = j(m) и все они принадлежат k-элементному множеству M1 = {a1 , … , ak}. Это значит, что r1 , … , rk – это те же числа a1 , … , ak , возможно, в другом порядке. Поэтому
a1× … ×ak = r1× … ×rk º b1× … ×bk = (a×a1)× … ×(a×ak) = ak×a1× … ×ak (mod m).
Значит, a1× … ×ak º ak×a1× … ×ak (mod m), (aj(m) – 1)×a1× … ×ak (mod m). Учитывая, что a1× … ×ak взаимно просто с m (т.к. все ai взаимно просты с m), получим по свойствам сравнений aj(m) – 1 º 0 (mod m).
Теорема Эйлера доказана.
Упражнение.Пусть m = 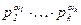 – каноническое разложение натурального числа m,
– каноническое разложение натурального числа m, 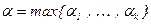 . Тогдадля любого целого числа a выполнено сравнение aa×(aj(m) – 1)) º 0 (mod m).
. Тогдадля любого целого числа a выполнено сравнение aa×(aj(m) – 1)) º 0 (mod m).
Теорема (малая теорема Ферма).Для любого простого числа p и целого числа a , не делящегося на p, имеет место сравнение a p–1 º 1 (mod p).
Доказательствоследует из теоремы Эйлера при m = p с учётом равенства j(p) = р – 1.
Следствие.Для любого простого числа p и целого a верно сравнение a p º a (mod p).
Доказательство следует из теоремы Ферма: a p – a º a×(a p–1 – 1) º 0 (mod p) как для a, делящегося на p, так и для взаимно простого с p.
Упражнения: 1.Докажите, что для любого целого a выполняется сравнение a561 º a (mod 561), но число 561 – не простое. Таким образом, обращение теоремы Ферма не верно.
2. Докажите, что 561 – наименьший контрпример к обращению теоремы Ферма.
Теоремы Эйлера и Ферма можно использовать для нахождения остатков некоторых арифметических выражений, значения которых трудно вычислить.
I. Остатки полиномиальных выражений.Пусть требуется найти остаток от деления на заданное число m некоторого выражения P(a1 , … , an), полученного из целых чисел а1 , … , аn с помощью операций сложения, вычитания и умножения.
Для решения этой задачи достаточно, исходя из значений аi (mod m), найти значение P(a1 , … , an) по модулю m.
Примеры: 1.Найти остаток от деления 123×349 – 88×560 + 8932 на 4.
Вычислим значения всех участвующих в данном равенстве чисел по модулю 4: 123 º –1 (mod 4), 349 º 1 (mod 4), 88 º 0 (mod 4), 893 º 1 (mod 4). Поэтому по свойствам сравнений имеем
123×349 – 88×560 + 8932 º (–1)×1–0×560+12 = 0 (mod 4).
Значит, исходное выражение делится на 4, т.е. искомый остаток равен 0.
2. Найти остаток от деления на 6 выражения
–3356×299 – 3338×5551 – 325×(–287 + 679×825).
Имеем 3356 º 2 (mod 6), 299 º –1 (mod 6), 333 º 3 (mod 6), 5551 º 1 (mod 6), 325 º 1 (mod 6), 287 º –1 (mod 6), 679 º 1 (mod 6), 825 º 3 (mod 6). Поэтому получаем
–3356×299–3338×5551–325×(–287+679×825) º –2×(–1)–(32)4×1–1×(–(–1)+1×3) º
º 2–(32)2–(–2) º 2–32+ 2 º –5 º 1 (mod 6),
т.е. искомый остаток равен 1.
II. Остатки экспоненциальных выражений.Пусть требуется найти остаток от деления на число m некоторого выражения P(a1 , … , an), полученного из целых чисел а1 , … , аn с помощью операций сложения, вычитания, умножения и возведения в большие степени.
Как и ранее, для решения этой задачи достаточно, исходя из значений аi (mod m), вычислить P(a1 , … , an) (mod m). При вычислении степенных выражений с большими показателями степеней удобно пользоваться теоремами Эйлера и Ферма.
Примеры: 1.Найти остаток от деления числа 3546 – 88 на 5.
Так как НОД(3, 5) = 1, то по теореме Эйлера, 3j(5) º 1 (mod 5) или 34 º 1 (mod 5), поскольку j(5) = 4. Значит, 3546 = (34)136×32 º 1136×32 º º 9 º 4 (mod 5), и 3546 – 88 º 4 – 3 º 1 (mod 5), так что искомый остаток равен 1.
2. Найти последнюю цифру числа 7 954.
Заметим, что для заданного числа a = 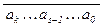 в десятичной системе счисления, выполняется сравнение
в десятичной системе счисления, выполняется сравнение 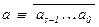 (mod 10 s):
(mod 10 s):
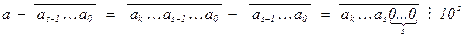 .
.
Таким образом, для нахождения s последних цифр числа a достаточно найти остаток от деления его на 10 s. В данном примере нужно искать остаток от деления числа 7 954 на 10.
Поскольку НОД(7, 10) = 1, то можно воспользоваться теоремой Эйлера: 7j(10) º 1 (mod 10). Вычисляем j(10) = j(2×5) = j(2)×j(5) = 1×4 = 4 и получаем: 74 º 1 (mod 10).
Поэтому 7 954 = (74)238×72 º 1238×72 = 49 º 9. Итак, последняя цифра числа 7 954 равна 9.
3. Найти две последние цифры числа 8 345.
Здесь нужно искать остаток от деления числа 8 345 на 100 = 102.
Поскольку НОД(8 345, 100) = НОД(2 3×345, 22×52) = 22 = 4 ¹ 1, непосредственно воспользоваться теоремой Эйлера нельзя. Если 8 345 = 4×y , то 8 345 º º 4×y (mod 100) Û 4×2×8344 º 4×y (mod 100) Û 2×8344 º y (mod 25), причём 8 уже взаимно просто с 25, и можно использовать теорему Эйлера: 8j(25) º 1 (mod 25). Поскольку j(25) = j(52) = 52 – 51 = 20, то
8 344 º (8 20) 17×8 4 º 117×(8 2) 2 º 14 2 = 196 º –4 (mod 25).
Таким образом, y º 2×8 344 º 2×(–4) = –8 º 17 (mod 25), и 8 345 = 4×y º º 4×17 = 68 (mod 100). Итак, число 8 345 оканчивается на 68.
4.Найти две последние цифры числа 6 34 – 358.
Действуем аналогично предыдущему: поскольку НОД(6 34, 100) = 4, имеем 6 34 = 4×x, 6 34 º 4×x (mod 100) Û 32×6 32 º x (mod 25) и 6 20 º 1 (mod 25), так что x º 32×6 32 º 32×6 12 º 9×36 6 º 9×11 6 º 9×121 3 º 9×(–4)3 º º –9×64 º –9×14 = –126 º –1 (mod 25) и 6 34 º 4×(–1) = –4 º 21 (mod 100).
Значительно проще найти остаток от второго слагаемого: 3 j(100) º 1 (mod 100), т.е. 3 40 º 1 и 3 58 º 3 18 = 81 4×3 2 º 19 4×3 2 º 61 2×3 2 = 183 2 º º (–17) 2 = 289 º 89 (mod 100). Таким образом, 6 34 – 358 º 21 – 89 = – 68 º º 32 (mod 100), т.е. исходное число оканчивается на 32.
Признаки делимости
Признак делимости на число m Î N– это такая процедура (алгоритм), которая сводит задачу о делимости данного большого числа на m к аналогичной равносильной задаче для гораздо меньшего числа. Например, признак делимости на 2 утверждает, что число делится на 2 тогда и только тогда, когда делится на 2 последняя (младшая) цифра этого числа. Таким образом, вместо самого многозначного числа признак делимости на 2 рекомендует делить на 2 только одну цифру.
Из школьного курса известны признаки делимости на 2, 4, 5, 25, 3, 9. Оказывается, что все они укладываются в одну схему.
Пусть даны натуральные число m , и число k = 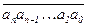 , записанное в десятичной системе счисления, b0 , … , bn – фиксированные целые числа, причём bi º 10i (mod m) (0 £ i £ n). Целое число m(k) = an×bn + … + a1×b1 + a0×b0 (mod m) назовём т-индикатором числа k .
, записанное в десятичной системе счисления, b0 , … , bn – фиксированные целые числа, причём bi º 10i (mod m) (0 £ i £ n). Целое число m(k) = an×bn + … + a1×b1 + a0×b0 (mod m) назовём т-индикатором числа k .
Примеры: 1. Пусть m = 3, bi = 1 (0 £ i £ n). Тогда имеем 10i º 1i = bi (mod 3). Поэтому выражение 3(k) = an + …+ a0 является 3-индикатором числа k = 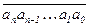 .
.
2. В предыдущем примере можно было бы взять и другие числа bi , например, bi = 4 (0 £ i £ n) также годятся, т.к. 4 º 1 (mod 3). Поэтому выражение 3(k) = 4×an + …+ 4×a0 тоже является 3-индикатором числа k = 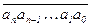 .
.
3.Проверьте самостоятельно, что 9(k) = an + …+ a0 является 9-индикатором числа k = 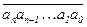 .
.
Приведённые примеры показывают, что т-индикаторы определены не однозначно – они зависят от конкретного выбора чисел bi (0 £ i £ n),в качестве которых всегда можно взять, например, остатки от деления чисел 10i на т.
Теорема (обобщённый признак делимости Паскаля).Пусть заданы произвольное натуральное число m и число k = 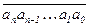 в десятичной системе счисления. Тогда k º m(k) (mod m). В частности, k M m тогда и только тогда, когда m(k) M m.
в десятичной системе счисления. Тогда k º m(k) (mod m). В частности, k M m тогда и только тогда, когда m(k) M m.
Доказательство. Ввиду 10i º bi (mod m) имеем
k = 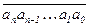 = an×10n + an–1×10n–1 + … + a1×10 + a0 º
= an×10n + an–1×10n–1 + … + a1×10 + a0 º
º an×bn + an–1×bn–1 + … + a1×b1 + a0×b0 = m(k) (mod m).
В частности, k M m Û k º 0 (mod m) Û m(k) º 0 (mod m) Û m(k) M m.
Теорема доказана.
Следствие 1 (известные признаки делимости).Для числа k = 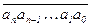 справедливы следующие утверждения:
справедливы следующие утверждения:
(1) для любого s (1 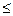 s
s 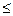 n) верно k
n) верно k 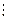 2s Û
2s Û 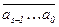 M 2s ,
M 2s ,
(2) для любого s (1 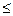 s
s 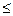 n) верно k
n) верно k 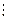 5s Û
5s Û 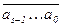 M 5s ,
M 5s ,
(3) k M 3 Û (an + … + a0) M 3,
(4) k M 9 Û (an + … + a0) M 9,
(5) k M 11 Û (an  (–1)n + … + ai
(–1)n + … + ai  (–1)i + … + a0) M 11.
(–1)i + … + a0) M 11.
Доказательство.(1), (2) Обозначая через m числа 2s или 5s (в зависимости от доказываемого утверждения), имеем 10i º 10i (mod m ) при i < s и 10i º 0 (mod m) при i ³ s. Поэтому, если в обобщённом признаке делимости Паскаля положить bi = 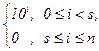 , то
, то
k M т Û (an  0 + … + as
0 + … + as  0 + as–1
0 + as–1  10s–1 + … + a0
10s–1 + … + a0  100) M т Û
100) M т Û 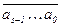 M т.
M т.
(3), (4) Снова, обозначая через m числа 3 или 9 (в зависимости от доказываемого утверждения), получим 10i º 1 (mod m), так что всё следует из признака делимости Паскаля.
(5) Легко видеть, что 10i º (–1)i (mod 11), т.е. в качестве bi в признаке делимости Паскаля можно взять (–1)i.
Следствие 1 доказано.
Следствие 2 (признак делимости на 7). Для числа k = 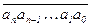 выполнены следующие утверждения:
выполнены следующие утверждения:
(1) трёхзначное число k = 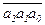 делится на 7 тогда и только тогда, когда 7(k) = a0 + 3×a1 + 2×a2 делится на 7,
делится на 7 тогда и только тогда, когда 7(k) = a0 + 3×a1 + 2×a2 делится на 7,
(2) если число k разбито справа налево на грани gi = 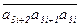 по три десятичных цифры в каждой (0 £ i £
по три десятичных цифры в каждой (0 £ i £ 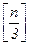 + 1), то k M 7 в том и только том случае, когда (g0 – g1 + … + (–1)igi + …) M 7,
+ 1), то k M 7 в том и только том случае, когда (g0 – g1 + … + (–1)igi + …) M 7,
(3) в условиях утверждения (2) k M 7 в том и только том случае, когда (7(g0) – 7(g1) + … + (–1)i×7(gi) + …) M 7.
Доказательство.(1) следует непосредственно из признака делимости Паскаля при b0 = 1 º 100, b1 = 3 º 101, b2 = 2 º 102 (mod 7).
(2) Ясно, что выполнено равенство k = g0 + g1×103 + g2×106 + … , причём, 103 = 7×143 – 1 º –1 (mod 7). Поэтому 103×i º (–1)i и, как и при доказательстве признака делимости Паскаля,
k = g0 + g1×103 + g2×106 + … º g0 – g1 + … + (–1)igi + … (mod 7).
(3) Положим b6×i = 1, b6×i+1 = 3, b6×i+2 = 2, b6×i+3 = –1, b6×i+4 = –3, b6×i+5 = –2 (i Î N0). Тогда можно убедиться, что 10s º bs (mod 7). Значит
7(k) = a0×b0 + … + an×bn =
= (a0×1 + a1×3 + a2×2)–(a3×1 + a4×3 + a5×2)+…+(–1)i×(a3×i×1 + a3×i+1×3 + a3×i+2×2)+… = = 7(g0) – 7(g1) + … + (–1)i×7(gi) + … .
Следствие 2 доказано.
Примеры: 1.Делится ли на 7 число 89653421567 ?
89.653.421.567 = 089.653.421.567 º 567 – 421 + 653 – 089 º
º (1×7 + 3×6 + 2×5) – (1×1 + 3×2 + 2×4) + (1×3 + 3×5+ 2×6) – (1×9 + 3×8 + 2×0) º
º 0 – 1 + 2 – 5 = –4 º 3 (mod 7).
Таким образом, число даёт остаток 3 при делении на 7, и не делится на 7.
2.Делится ли на 7 число 82936455364728195106114 ?
| gi | 082 | 936 | 455 | 364 | 728 | 195 | 106 | 114 |
| 7(gi) | –2 | –2 | 0 | 0 | 0 | –1 | 1 | 2 |
| 7(k) | –(–2)+(–2)–0+0–0+(–1)–1+2 = 0 |
Итак, исходное число делится на 7.
Упражнение: Сформулируйте признаки деления на 13, 15, 27.
Замечание. Признаки делимости не всегда удобно формулировать, конструируя m-индикаторы. Хотя, как правило, удачно выбранный m-индикатор и минимизирует вычисления (что особенно важно при программировании на ЭВМ), но расплачиваться приходится трудностью запоминания получающихся признаков делимости, в чём читатель уже имел возможность убедиться, изучив признак делимости на 7. Следующая теорема показывает альтернативный путь – пусть менее короткий для вычислений, но зато более запоминающийся.
Теорема (признаки делимости на 7, 11, 13).Число k = 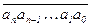 с количеством цифр n ³ 3 делится на 7, 11, 13 тогда и только тогда, когда на эти числа делится разность чисел, записанных его старшими (n – 3)-мя цифрами и младшими 3-мя цифрами соответственно.: если m Î {7, 11, 13}, то
с количеством цифр n ³ 3 делится на 7, 11, 13 тогда и только тогда, когда на эти числа делится разность чисел, записанных его старшими (n – 3)-мя цифрами и младшими 3-мя цифрами соответственно.: если m Î {7, 11, 13}, то 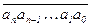 M m Û (
M m Û ( 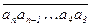 –
– 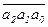 ) M m .
) M m .
Доказательство. Всё следует из a×1000 + b º –a + b (mod m).
Теорема доказана.
Упражнение: Докажите, что 10×a + b M 11 Û b – a M 11, 10×a + b M 19 Û Û a + 2b M 19.
Принцип Дирихле
Тема этого параграфа напрямую, казалось бы, не связана с арифметикой. Тем не менее, простые но не тривиальные соображения Дирихле используются во многих теоретико-числовых рассуждениях.
Принцип Дирихле: Если есть m куч, в которых содержится N объектов, то найдётся куча с числом объектов не менее N / m и куча с числом объектов не более N / m .
Доказательство. От противного. Если во всех кучах меньше N / m объектов, то всего объектов меньше m×(N / m) = N – противоречие.
Если во всех кучах больше N / m объектов, то всего объектов больше m×(N / m) = N – противоречие.
Принцип Дирихле доказан.
Как ни странно, этот простой принцип имеет глубокие применения. Прежде чем к ним переходить, решим несколько простых задач.
Задача 1. В студенческой группе 25 студентов. Доказать, что по крайней мере у трёх студентов дни рождения в одном месяце.
Будем раскладывать студентов по двенадцати кучам в соответствии с месяцами их дней рождения. По принципу Дирихле в одной из этих куч будет не менее 25 / 12 = 2,008… студентов. Поскольку дробных студентов не бывает, то в этой куче не менее трёх студентов.
Задача 2. В классе 28 человек. В диктанте хулиган Вовочка сделал 13 ошибок, а остальные – меньше. Докажите, что по крайней мере 3 ученика сделали равное число ошибок.
Учеников будем раскладывать по кучам в соответствии с количеством сделанных ими ошибок. Таких куч 14 (ошибок может быть от 0 до 13), причём в последней только один человек – хулиган Вовочка. Значит, в остальных тринадцати – 27 человек. По принципу Дирихле, в какой-то куче будет не менее 27 / 13 = 2,007… учеников, т.е. не менее трёх.
Задача 3. В доме 123 жильца, которым в сумме 3813 лет. Можно ли выбрать 100 из них, которым вместе не меньше 3100 лет ?
Достаточно понять, будет ли вместе не меньше 3100 лет ста самым старшим ? Предположим, что ста самым старшим в сумме менее 3100 лет. Тогда оставшимся двадцати трём в сумме не менее 3813 – 3100 = 713 лет. Если эти года раскладывать эти годы (объекты) по двадцати трём кучам (жильцам), то одна из куч по принципу Дирихле будет содержать не менее 713 / 23 = 31 объектов. Это значит, что возраст одного из оставшихся двадцати трёх человек не менее 31 года. Значит, самым старшим ста жильцам не менее 31 года каждому и их суммарный возраст не менее 3100 лет – противоречие.
Задача 4. Докажите, что в любой компании из п ³ 2 человек найдутся двое, имеющие одинаковое число знакомых (считаем, что каждый знаком, по крайней мере, сам с собой и если a знаком с b, то b знаком с a).
Количество знакомых у каждого может быть от 1 до n. Если раскладывать людей по кучам в соответствии с числом их знакомых, то в n куч разложатся n человек. Если предположить, что в каждой куче по одному человеку, то будет знакомый со всеми n, а значит, не будет человек, знакомого с только с одним человеком – противоречие.
Задача 5. В строку выписано п целых чисел. Докажите, что сумма нескольких рядом стоящих из них делится на п.
Пусть числа a1 , … , an . Рассмотрим последовательные суммы b1 = a1 , b2 = a1 + a2 , … , bi = a1 + … + ai , … , bn = a1 + … + an . Нужно доказать, что одно из bi делится на n, т.е. даёт остаток 0 при делении на n. Предположим, что остаток 0 не даёт ни одно из них. Тогда их n, а ненулевых остатков – (n – 1). Ясно, что по принципу Дирихле среди них два bi и bj при i > j дают один и тот же остаток. Значит, bi – bj = ai + ai–1 + … + aj+1 M n, что и требовалось.
Задача 6. Двоечник Вовочка выучил только одну цифру – единицу. Сможет ли он с её помощью записать число, делящееся на c = 10×2021 + 1 ?
Рассмотрим бесконечную последовательность чисел 1, 11, … , 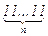 , … , записываемых одними единицами. Если раскладывать их по кучам – остаткам от деления на c , то в какой-то куче будет два числа .
, … , записываемых одними единицами. Если раскладывать их по кучам – остаткам от деления на c , то в какой-то куче будет два числа . 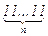 и
и 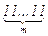 при n > m. Значит,
при n > m. Значит, 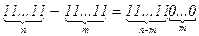 M c. Поскольку НОД(с, 10) = 1, то
M c. Поскольку НОД(с, 10) = 1, то 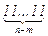 M с, так что Вовочка сможет записать нужное число одними единицами.
M с, так что Вовочка сможет записать нужное число одними единицами.
Задача 7. Докажите, что существует степень числа 13, оканчивающаяся на 00000001.
Рассмотрим степени 131 , 132 , … , 13i , … Нужно доказать, что среди них есть число 13k º 1 (mod 108). По принципу Дирихле среди них есть два, имеющих одинаковые остатки при делении на 108 : 13i º 13j (mod 108) при i > j, т.е. 13j×(13i–j – 1) M 108. Значит, можно взять k = i – j (?!).
Задача 8. В единичный квадрат бросили 50 точек. Доказать, что найдутся две из них, отстоящие друг от друга на расстояние не более 0,3.
Разобьём квадрат на равные 49 квадратиков, проведя прямые, параллельные сторонам квадрата. Тогда какие-то две точки попали в один квадрат, т.е. расстояние между ними не более длины диагонали квадратика, которая равна 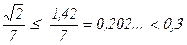 .
.
Задача 9. На складе имеется по 200 сапог 41-го, 42-го и 43-го размеров, причём среди всех 600 сапог есть 300 левых и 300 правых. Докажите, что можно обуть не менее 100 человек.
Если обуто менее ста человек, то на это пошло менее двухсот сапог, а значит, осталось более 400 сапог. Среди них поровну левых и правых, но нет левых и правых одного размера, иначе можно было бы ещё кого-нибудь обуть. Из этих оставшихся более чем 400 сапог будет левых и правых поровну и более чем по 200. Ни левые, ни правые не могут быть одного размера (общее количество сапог одного размера равно 200). Значит, среди левых есть сапоги, по крайней мере, двух размеров. Точно так же и среди правых есть сапоги, по крайней мере, двух размеров. Но тогда есть левые и правые одного размера – противоречие.
Задача 10. Даны пять точек на плоскости с целыми координатами. Доказать, что середина одного из отрезков, соединяющего две из них, тоже имеет целые координаты.
Докажем, что среди этих точек есть две, обе координаты которых одной чётности: если это точки M(a; b) и N(c; d), то середина отрезка MN имеет координаты 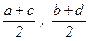 Î Z .
Î Z .
Рассмотрим координаты точек по модулю 2. Тогда они могут иметь один из четырёх видов (0; 0), (0; 1), (1; 0), (1; 1). Если точек пять, то у двух из них M(a; b) и N(c; d) получатся одинаковые координаты по модулю 2. Эти точки искомые.
Теперь докажем более серьёзное утверждение:
Лемма (о приближении действительных чисел рациональными). Для любого действительного числа r > 0 и произвольного n Î N найдутся натуральные числа a, b Î N, где 1 £ b £ n со свойством |b×r – a| £ 
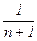 .
.
Доказательство. Разобьём отрезок [0; 1] на n равных частей точками 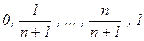 и рассмотрим последовательность чисел {0×r}, {1×r}, {2×r}, … , {n×r}, 1, где {x} = x – [x] – дробная часть числа x. Все члены последовательности принадлежат отрезку [0; 1], и каждый из них попадает в какой-то интервальчик
и рассмотрим последовательность чисел {0×r}, {1×r}, {2×r}, … , {n×r}, 1, где {x} = x – [x] – дробная часть числа x. Все члены последовательности принадлежат отрезку [0; 1], и каждый из них попадает в какой-то интервальчик 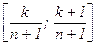 (0 £ k £ n). Поскольку таких интервалов только n+1, а рассматриваемых чисел n+2, то два из них попадут в один и тот же интервальчик. Либо {i×r}, {j×r} Î
(0 £ k £ n). Поскольку таких интервалов только n+1, а рассматриваемых чисел n+2, то два из них попадут в один и тот же интервальчик. Либо {i×r}, {j×r} Î 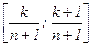 при 0 £ i < j£ n, т.е. |{i×e} – {j×r}| £
при 0 £ i < j£ n, т.е. |{i×e} – {j×r}| £ 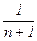 и значит,
и значит,
|(i×r – [i×r]) – (j×r – [j×r])| = |(i – j)×r – ([j×r] – [i×r])| = |b×r – a| £ 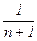 ,
,
где 0 £ b = i – j £ n, a = [j×r] – [i×r] Î Z . Либо {i×r}, 1 Î 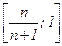 , т.е. будет |{i×r} – 1| £
, т.е. будет |{i×r} – 1| £ 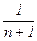 и значит, |i×r – [i×r] – 1| = |b×r – a| £
и значит, |i×r – [i×r] – 1| = |b×r – a| £ 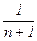 , где 0 £ b = i £ n,
, где 0 £ b = i £ n,
a = [i×r] – 1 Î Z . В любом случае |b×r – a| £ 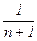 при 0 £ b £ n, a Î Z.
при 0 £ b £ n, a Î Z.
Лемма доказана.
Аналогично можно доказать следующее любопытное утверждение:
 По окружности длины 1 из любой точки Н начинает в одну сторону прыгать кузнечик на расстояние
По окружности длины 1 из любой точки Н начинает в одну сторону прыгать кузнечик на расстояние 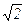 . Тогда через несколько прыжков он обязательно попадёт в канавку Кпроизвольной ширины e .
. Тогда через несколько прыжков он обязательно попадёт в канавку Кпроизвольной ширины e .
Более общо:
Лемма (о кузнечике). Для любого иррационального числа a , действительного s и положительного e найдутся такие целые числа a, b, что
|b×a – s – a| < e.
Доказательство. Пусть кузнечик прыгает против часовой стрелки от точки Н на окружности длины 1 канавкой ширины e на расстоянии s от Н, преодолевая за один скок расстояние a.
Во-первых, некоторые следы кузнечика окажутся на расстоянии меньше e. Действительно, разобьём окружность на равные части длины 1 / N < e . Тогда по принципу Дирихле через более N прыжков некоторые два следа с номерами k, k + p попадут в одну из замкнутых частей, т.е. выполняется неравенство |(k + p)×a – k×a – a| < e Û |p×a – a| < e для некоторого целого a. При этом ввиду иррациональности a разность p×a – a не равна нулю.
 Во-вторых, на расстоянии меньше e будут и следы с номерами k + p и k + 2×p, k + 2×p и k + 3×p, … , k + i×p, k + (i+1)×p (i Î N):
Во-вторых, на расстоянии меньше e будут и следы с номерами k + p и k + 2×p, k + 2×p и k + 3×p, … , k + i×p, k + (i+1)×p (i Î N):
|(k + (i+1)×p)×a – (k + i×p)×a – a| < e Û |p×a – a| < e .
Таким образом, следы с номерами k, k+p, k+2×p, … следуют по окружности через одно и то же расстояние 0 < d < e . Значит эти следы (в какую бы сторону по окружности они ни шли), обязательно дойдут до канавки, а перепрыгнуть через неё не смогут.
Лемма доказана.
Доказанные леммы имеют весьма неочевидные применения:
Задача: Доказать, что степени двойки могут начинаться на любую комбинацию цифр.
Пусть N – число, десятичная запись которого представляет заданную комбинацию цифр. Нужно найти такие натуральные числа n, r, что
N×10r < 2n < (N + 1)×10r.
Это равносильно неравенствам r + lg N < n×lg 2 < r + lg(N + 1). Отнимая от всех чисел середину 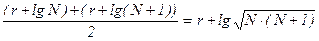 рассматриваемого отрезка (r + lg N ; r + lg(N + 1)), получим
рассматриваемого отрезка (r + lg N ; r + lg(N + 1)), получим
|n×lg 2 – r – 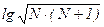 | <
| < 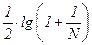 .
.
Это выполняется по лемме о кузнечике при иррациональном a = lg 2 , вещественном s = 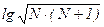 и положительном e =
и положительном e = 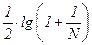 .
.
Дата добавления: 2021-12-14; просмотров: 818;











