Степень подвижности и структура плоских механизмов

Определив число звеньев, а также число и типы кинематических пар, можно рассчитать степень подвижности W механизма. Для плоских механизмов по формуле Чебышева:

W = 3n – 2p₅ – p₄ . (1.3)

где n – число подвижных звеньев; р₅ – число пар пятого класса; р₄ – число пар четвертого класса.

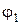Степень подвижности соответствует числу степеней свободы механизма относительно стойки и определяет число независимых обобщенных координат, необходимых для задания положения всех звеньев механизма. Для механизма грохота, рис.2, , следует задать одну обобщенную координату, например, зависимость от времени угла поворота звена 1. В этом случае звено 1 называется начальным, так как определение положения всех звеньев механизма начинается с определения положения этого звена. Отметим, что начальное звено может и не совпадать с входным звеном, движение которого задано двигателем.

Стойку и начальное звено, соединенные кинематической парой, условно называют начальным механизмом (рис. 2, б). Более сложные механизмы образуются путем последовательного присоединения к начальному механизму структурных групп или групп Ассура. Структурная группа входит в механизм вместе со своими кинематическими парами: внутренними, соединяющими звенья группы, и внешними, с помощью которых группа присоединяется к механизму. Основным признаком структурной группы является то, что она не изменяет степень подвижности механизма. Так как начальный механизм уже имеет степень подвижности 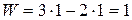, которая равна числу степеней свободы всего механизма, то группа Ассура должна иметь степень подвижности, равную нулю. Тогда для группы, входящей в плоский механизм с парами пятого класса из формулы (1.3) следует условие

W_rp = 3 n – 2 p₅ = 0 или р₅ = 3/2 п. (1.4)

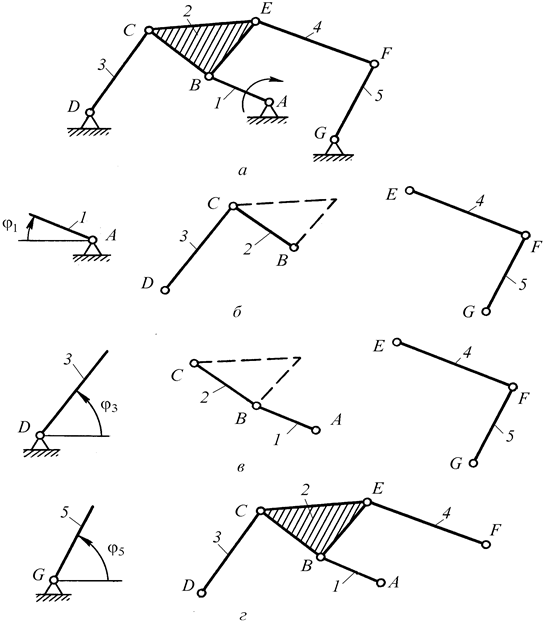
Рис. 3. Зависимость класса механизма от выбора начального звена:

а – структурная схема механизма; б, в – начальный механизм и две группы Ассура II класса, 2 порядка; г – начальный механизм и группа Ассура III класса,

3 порядка

Таким образом, число пар в группе Ассура в полтора раза больше числа звеньев, а число звеньев должно быть четным, так как р₅ –целое число. Самые простые группы содержат два звена и три кинематические пары (группы звеньев 2–3 и 4–5 на рис. 2, в, г и группы 2–3 и 4–5 на рис. 3, б). По классификации Л. В. Ассура – И. И. Артоболевского класс группы Ассура равен числу кинематических пар, входящих в самый сложный замкнутый контур, образованный внутренними парами. Группа звеньев 1–2–3–4 на рис. 3, г является группой Ассура третьего класса. Двухзвенные группы отнесены ко второму классу. Классом самой сложной группы Ассура определяется класс всего механизма.

Число внешних кинематических пар определяет порядок группы Ассура. Все группы второго класса являются группами второго порядка, группа Ассура на рис. 3, г – третьего порядка.

Введение понятия о структурных группах удобно тем, что группа Ассура является статически определимой системой; число уравнений равновесия для сил, приложенных к звеньям, равно числу неизвестных реакций в кинематических парах группы. Это свойство группы используется при силовом расчете механизма. Кроме того, кинематическое исследование механизма проводится в порядке присоединения групп к начальному звену.

Часто классы групп Ассура, их число и класс механизма зависят от выбора начального звена. Если, например, в механизме на рис. 3, а в качестве начального выбрать звено 3, то выделяются две группы второго класса (рис. 3, в). Если начальным звеном является звено 5 (рис. 3, г), то механизм включает в себя одну группу третьего класса. Чем выше класс механизма, тем сложнее его кинематический и силовой анализ. Поэтому целесообразно выбирать начальное звено по возможности так, чтобы при анализе получался механизм второго класса.

Разложение механизма на группы Ассура производят в порядке, обратном их присоединению. Выбрав начальное звено, сначала пытаются выделить наиболее отдаленную от него группу, предполагая, что она второго класса, т.е. состоит из двух звеньев с одной внутренней и двумя внешними кинематическими парами. При этом оставшиеся звенья должны по-прежнему составлять механизм. Если это условие выполняется, то из оставшегося механизма выделяют следующую группу. Если же не выполняется (оставшиеся звенья образуют разомкнутые цепи), значит выделяемая структурная группа не второго класса, а более сложная.