Перекатывающийся груз
Пусть на судне находится твердый груз, который при наклонении в некоторой плоскости перекатывается так, что его ЦТ перемещается в той же плоскости по кривой из точки B в точку B1 (рис. 2.17, б). Для каждого угла наклонения сила тяжести груза действует по нормали к кривой BB1 в соответствующей точке, причем эта нормаль перпендикулярна плоскости действующей ватерлинии. Если точка B отвечает положению равновесия судна, а точка B1 — наклонению на малый угол 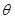 , то линии действия силы тяжести груза для этих двух положений пересекутся в некоторой точке A. Но в этой же точке пересекутся соответствующие нормали к кривой BB1, поэтому в пределе при бесконечно малом угле наклонения точка A является центром кривизны кривой BB1 в точке B.
, то линии действия силы тяжести груза для этих двух положений пересекутся в некоторой точке A. Но в этой же точке пересекутся соответствующие нормали к кривой BB1, поэтому в пределе при бесконечно малом угле наклонения точка A является центром кривизны кривой BB1 в точке B.
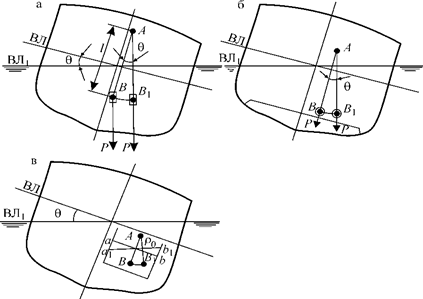
Рис. 2.17. К оценке влияния на остойчивость: а — подвешенного; б — перекатывающегося; в — жидкого грузов
Сопоставляя рисунки (2.17, а) и (2.17, б), легко убедиться, что перека-тывающийся груз оказывает точно такое же влияние на начальную остойчивость, как и груз, подвешенный в точке A. Положение этой точки определим радиусом кривизны l кривой, по которой перекатывается груз в данной плоскости наклонения. По аналогии с поправкой к метацентрической высоте, обусловленной перемещением подвешенного груза [см. формулу (2.67)], снижение поперечной метацентрической высоты от влияния перекатывающегося груза будет равно
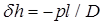 . (2.70)
. (2.70)
Его можно также трактовать, как результат переноса ЦТ груза в точку A — центр кривизны кривой BB1. Следовательно, изменение аппликаты ЦТ судна равно
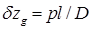 . (2.71)
. (2.71)
Значение радиуса кривизны l зависит от вида кривой перекатывания BB1, т. е. от формы опорной поверхности, по которой катится груз. В частном случае, когда эта поверхность является плоскостью, радиус кривизны l равен бесконечности при любом виде наклонения. Раскрепление груза, способного перекатываться, в этом случае приводит согласно формуле (2.70) к бесконечно большому снижению начальной метацентрической высоты, независимо от величины груза p. Таким образом, мы приходим к, казалось бы, парадоксальному факту полной потери начальной остойчивости при перекатывании самого малого груза. В действи-тельности этот факт объясняется достаточно просто. В момент раскрепления и начала перекатывания груза метацентрическая высота действительно стремится к бесконечности, положение равновесия судна оказывается неустойчивым, и оно начинает заваливаться на борт. Груз при этом перекатывается и останавливается у первого же препятствия на своем пути, после чего он должен рассматриваться уже как закрепленный. Остойчивость судна становится положительной, практически такой же, что и до перекатывания груза, поскольку его перемещение можно трактовать как перенос в горизонтальной плоскости. Новое положение равновесия судна определится углом крена или дифферента, определяемым по формулам (2.62), в зависимости от плоскости наклонения. Значение этого угла зависит от соотношения между массой перекатавшегося груза и водоизмещением (массой) судна. Если груз относительно мал, то и угол, с которым судно будет плавать в наклонном положении, окажется ничтожным. Вообще же формулы (2.70) и (2.71) справедливы как для малого, так и большого груза не только при поперечных, но и при продольных наклонениях судна.
Жидкий груз
Пусть на судне в цистерне, танке или отсеке имеется какой-либо жидкий груз. Если этот груз заполняет емкость, например, отсек, целиком, то при наклонении судна он переливаться не будет, его ЦТ останется на месте и в расчете остойчивости такой груз может рассматриваться как твердый. Если же груз заполняет отсек лишь частично и жидкость в отсеке имеет свободную поверхность, то при наклонении судна она будет переливаться, ЦТ груза сместится и это вызовет перемещение ЦТ судна. Ясно, что остойчивость судна при этом изменится.
Рассмотрим вначале наклонение судна на угол 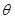 в поперечной плоскости (рис. 2.17, в). Введем обозначения: v — объем жидкости в отсеке,
в поперечной плоскости (рис. 2.17, в). Введем обозначения: v — объем жидкости в отсеке, 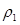 — ее плотность,
— ее плотность, 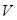 — объемное водоизмещение судна,
— объемное водоизмещение судна, 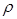 — плотность забортной воды. ПустьВ0Л0 — след ватерлинии судна в прямом положении, ВθЛθ — в наклонном, ab — след уровня жидкости в отсеке для прямого положения судна, a1b1 — для наклонного. Тогда ЦТ жидкого груза в отсеке при наклонении переместится из точки B в точку B1 по кривой BB1. Это перемещение вполне аналогично перемещению ЦВ судна, форма обводов которого совпадает с формой рассматриваемого отсека. Следовательно, кривая BB1 геометрически будет подобна кривой ЦВ на участке наклонения
— плотность забортной воды. ПустьВ0Л0 — след ватерлинии судна в прямом положении, ВθЛθ — в наклонном, ab — след уровня жидкости в отсеке для прямого положения судна, a1b1 — для наклонного. Тогда ЦТ жидкого груза в отсеке при наклонении переместится из точки B в точку B1 по кривой BB1. Это перемещение вполне аналогично перемещению ЦВ судна, форма обводов которого совпадает с формой рассматриваемого отсека. Следовательно, кривая BB1 геометрически будет подобна кривой ЦВ на участке наклонения 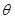 , а радиус кривизны кривой BB1 подобен метацентрическому радиусу судна, который определяется формулой (2.11):
, а радиус кривизны кривой BB1 подобен метацентрическому радиусу судна, который определяется формулой (2.11): 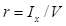 . Аналогично для радиуса кривизны кривой BB1 можно написать
. Аналогично для радиуса кривизны кривой BB1 можно написать
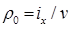 , (2.72)
, (2.72)
где 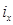 — момент инерции свободной поверхности жидкости в отсеке относительно ее центральной продольной оси, параллельной Ox.
— момент инерции свободной поверхности жидкости в отсеке относительно ее центральной продольной оси, параллельной Ox.
Перемещение ЦТ груза в сторону наклонения приводит к возникновению дополнительного кренящего момента. По аналогии с подвешенным грузом изменение метацентрической высоты будет равно
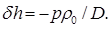 (2.73)
(2.73)
Подставляя сюда 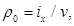
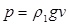 и
и 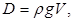 получим
получим
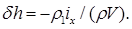 (2.74)
(2.74)
Величина 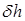 представляет собой поправку к поперечной метацентрической высоте, учитывающую влияние свободной поверхности жидкого груза в отсеке на начальную остойчивости. Все величины, входящие в правую часть (2.74), положительны, поэтому поправка
представляет собой поправку к поперечной метацентрической высоте, учитывающую влияние свободной поверхности жидкого груза в отсеке на начальную остойчивости. Все величины, входящие в правую часть (2.74), положительны, поэтому поправка 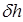 всегда отрицательна. Таким образом, жидкий груз со свободной поверхностью всегда уменьшает начальную остойчивость судна. Важно отметить, что поправка
всегда отрицательна. Таким образом, жидкий груз со свободной поверхностью всегда уменьшает начальную остойчивость судна. Важно отметить, что поправка 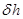 не зависит от объема жидкости в отсеке; она зависит только от момента инерции площади свободной поверхности и возрастает с его увеличением. Эта поправка тем больше, чем больше соотношение плотностей жидкости в отсеке и забортной воды. Если груз, например разжиженный железорудный концентрат, имеет плотность, значительно большую, чем у воды, остойчивость судна может существенно снизиться даже при сравнительно небольшой площади свободной поверхности.
не зависит от объема жидкости в отсеке; она зависит только от момента инерции площади свободной поверхности и возрастает с его увеличением. Эта поправка тем больше, чем больше соотношение плотностей жидкости в отсеке и забортной воды. Если груз, например разжиженный железорудный концентрат, имеет плотность, значительно большую, чем у воды, остойчивость судна может существенно снизиться даже при сравнительно небольшой площади свободной поверхности.
В случае, когда жидкие грузы со свободными поверхностями имеются в нескольких отсеках или цистернах, дополнительные кренящие моменты от их переливания суммируются и суммарная поправка к метацентрической высоте будет равна
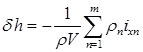 , (2.75)
, (2.75)
где m — число отсеков и цистерн, имеющих свободные поверхности жидкостей, которые могут быть различными.
Формула для поперечной метацентрической высоты, исправленной на влияние жидких грузов, имеет вид
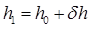 . (2.76)
. (2.76)
По аналогии с этим выражением исправленную продольную метацентрическую высоту можно определить как
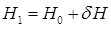 , (2.77)
, (2.77)
где
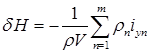 . (2.78)
. (2.78)
Здесь iyn — момент инерции свободной поверхности жидкости в отсеке относительно ее центральной поперечной оси, параллельной оси Oy. Для большинства надводных судов в неповрежденном состоянии поправка 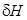 много меньше продольной метацентрической высоты H и в практических расчетах ее обычно не учитывают.
много меньше продольной метацентрической высоты H и в практических расчетах ее обычно не учитывают.
Для снижения влияния свободных поверхностей жидких грузов на поперечную остойчивость принимают следующие меры: заполнение трюма под самую палубу (запрессовка), чтобы не было свободной поверхности; отсек или цистерну разделяют продольными непроницаемыми переборками.
Предположим для простоты, что отсек имеет в плане форму прямоугольника длиной l и шириной b (рис. 2.18).
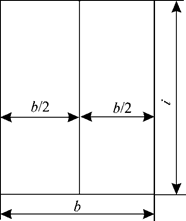
Рис. 2.18. Отсек с продольной непроницаемой переборкой
Момент инерции свободной поверхности жидкости относительно ее центральной продольной оси в таком отсеке равен 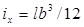 . Тогда поправка к метацентрической высоте на влияние свободной поверхности жидкого груза согласно (2.74) будет равна
. Тогда поправка к метацентрической высоте на влияние свободной поверхности жидкого груза согласно (2.74) будет равна
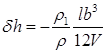 .
.
Установим посередине отсека продольную непроницаемую переборку. Момент инерции свободной поверхности жидкости в отсеке будет равен сумме моментов инерции двух площадей свободной поверхности шириной b/2 каждая:
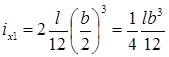 .
.
Соответственно поправка к метацентрической высоте
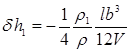
уменьшится в 4 раза.
Аналогичным образом легко показать, что при установке двух продольных переборок эта поправка уменьшится в 9 раз, а при установке n переборок в (n + 1)2 раз. Таким образом, разделение отсеков с жидкими грузами, имеющими свободную поверхность, непроницаемыми переборками является эффективным средством снижения влияния этих грузов на поперечную остойчивость судна.
На дне цистерн часто устанавливают отбойные листы в виде вертикальных продольных связей. Они играют ту же роль, что и продольные переборки в случае, когда жидкого груза в цистерне мало (остатки груза, отпотевание конструкций и т.д.).
При приеме на судно жидкого груза p, координаты ЦТ которого xp, yp, zp, изменение начальной остойчивости должно определяться с учетом влияния свободной поверхности. Добавляя в правую часть формулы (2.41) член, учитывающий это влияние в соответствии с (2.74), получим
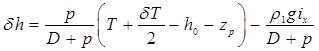 ,
,
где (D + p) — сила тяжести судна после приема груза. Подставляя 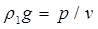 в правую часть этой формулы и вынося за скобку общий множитель
в правую часть этой формулы и вынося за скобку общий множитель 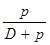 , находим
, находим
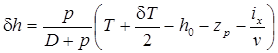 . (2.79)
. (2.79)
При полном расходовании жидкого груза со свободной поверхностью нужно не только считать 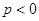 , но и положить равным нулю последний член в круглой скобке.
, но и положить равным нулю последний член в круглой скобке.
Изменение посадки судна в результате приема жидкого груза определяется непосредственно по формулам (2.49) — (2.56).
Сыпучий груз
При оценке остойчивости судов, перевозящих сыпучие грузы, не заполняющие отсеки целиком и имеющие свободную поверхность, считается, что каждому грузу соответствует некоторый угол покоя или угол естественного откоса 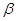 - максимальный угол наклона свободной поверхности по отношению к горизонту, при котором груз еще покоится, и превышение которого приводит к началу пересыпания груза. Величина угла естественного откоса зависит от рода груза, величины его частиц, от влажности, от вибраций судовых конструкций и т.д. В процессе перехода сыпучий груз может слеживаться, уплотняться.
- максимальный угол наклона свободной поверхности по отношению к горизонту, при котором груз еще покоится, и превышение которого приводит к началу пересыпания груза. Величина угла естественного откоса зависит от рода груза, величины его частиц, от влажности, от вибраций судовых конструкций и т.д. В процессе перехода сыпучий груз может слеживаться, уплотняться.
Если судно наклоняется на угол 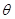 больше
больше 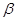 , происходит пересыпание до тех пор, пока поверхность груза опять не установится под углом естественного откоса. Считается, что пересыпание груза следует за его наклонением и свободная поверхность груза при пересыпании все время остается наклоненной к горизонту под углом покоя. Подобная схема, предложенная В.Г. Сизовым [29], достаточно близка к действительному процессу пересыпания для зерновых грузов, таких как пшеница, рожь, ячмень, овес, но она очень приближенная для оценки остой-чивости при перемещении таких грузов как достаточно крупный уголь и руда, пересыпание которых зачастую начинается с угла наклонения, большего угла естественного откоса, и сопровождается обрушиванием.
, происходит пересыпание до тех пор, пока поверхность груза опять не установится под углом естественного откоса. Считается, что пересыпание груза следует за его наклонением и свободная поверхность груза при пересыпании все время остается наклоненной к горизонту под углом покоя. Подобная схема, предложенная В.Г. Сизовым [29], достаточно близка к действительному процессу пересыпания для зерновых грузов, таких как пшеница, рожь, ячмень, овес, но она очень приближенная для оценки остой-чивости при перемещении таких грузов как достаточно крупный уголь и руда, пересыпание которых зачастую начинается с угла наклонения, большего угла естественного откоса, и сопровождается обрушиванием.
Следуя принятой схеме пересыпания (рис. 2.19) и проводя аналогию с влиянием жидкого груза, легко оценить влияние сыпучего груза на начальную поперечную остойчивость судна. При статическом действии некоторого кренящего момента Mкр дополнительный кренящий момент от воздействия пересыпающегося груза будет равен
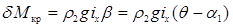 , (2.80)
, (2.80)
где 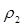 — плотность груза;
— плотность груза; 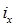 — момент инерции свободной поверхности груза в отсеке;
— момент инерции свободной поверхности груза в отсеке; 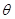 — малый угол крена судна;
— малый угол крена судна; 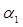 — угол покоя груза при крене на правый борт, когда
— угол покоя груза при крене на правый борт, когда 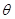 положителен.
положителен.
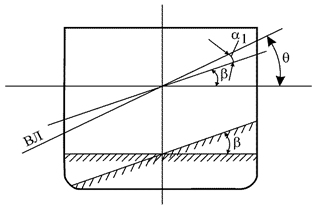
Рис. 2.19. Схема пересыпания зернового груза
Используя условие (2.80) и метацентрическую формулу поперечной остойчивости, найдем угол, на который накренилось судно:
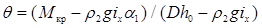 . (2.81)
. (2.81)
После прекращения действия Mкр судно уже не вернется в прямое положение, а будет плавать с некоторым остаточным углом крена, поскольку часть пересы-павшегося груза так и останется на борту, на который было наклонено судно.
Наличие остаточного угла крена при спрямлении судна является характерным отличием влияния на остойчивость сыпучего груза по сравнению с влиянием жидкого.
При повторном действии внешнего кренящего момента в ту же сторону образуется точно такой же угол крена 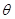 , но уже отсчитываемый от остаточного угла крена. После снятия кренящего момента возникает новый остаточный угол крена, который будет суммироваться с предыдущим, т.е. остаточный угол крена судна может накапливаться, и при неоднократном действии кренящего момента судно может даже опрокинуться.
, но уже отсчитываемый от остаточного угла крена. После снятия кренящего момента возникает новый остаточный угол крена, который будет суммироваться с предыдущим, т.е. остаточный угол крена судна может накапливаться, и при неоднократном действии кренящего момента судно может даже опрокинуться.
Чтобы избежать вредного воздействия сыпучего груза, можно предпринять следующие меры:
· заполнение трюма под самую палубу (запрессовка), чтобы не было свободной поверхности. Обычно произвести это весьма затруднительно, к тому же в процессе плавания груз слеживается и все равно возникает свободная поверхность;
· закрытие свободной поверхности брезентом и деревянными плоскими щитами (паёлами). Это не дает возможности двигаться верхним слоям сыпучего груза, что равносильно запрессовке;
· разделение свободной поверхности сыпучего груза подпалубными отбой-ными листами в виде вертикальных продольных связей. Эффект их воздействия подобен эффекту продольных переборок в цистернах с жидким грузом: уменьшение момента инерции свободной поверхности в (n+1)2 раз, где n – число отбойных листов.
Дата добавления: 2021-12-14; просмотров: 518;











