Свойства длины в евклидовых пространствах

1⁰. " v Î V |v| ³ 0, " v Î V |v| = 0 Û v = 0.

Оба утверждения выполнены ввиду свойства неотрицательности и свойства 3⁰ скалярного произведения.

2⁰. " v Î V " a Î R |a×v| = | 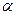|×|v|.

Это верно ввиду однородности скалярного произведения (?!).

3⁰. " u, v Î V |(u , v)| £ |u|×|v| – неравенство Коши-Буняковского-Шварца.

Действительно, пусть t – произвольное действительное число. Тогда, по свойствам скалярного произведения имеем:

0 £ (u+ t×v, u+ t×v) = (u, u) + 2×t×(u, v) + t²×(v, v).

Итак, полученный квадратный трёхчлен всюду неотрицателен. Поэтому его дискриминант неположителен: D = (2(u , v))² – 4(u, u)×(v, v) 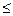0, т.е. (u, v)² £ £ (u, u)×(v, v) = (|u|×|v|)² ,что и требовалось.

4⁰. " u, v Î V | u + v| £ |u| + |v| – неравенство треугольника.

| u+v| £ |u| + |v| Û | u+v|² £ (|u| + |v|)² Û

Û (u+ v, u+ v) £ (u, u) + 2× 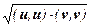+ (v, v) Û

Û (u, u)+2×(u,v)+(v, v) £ (u, u) + 2× 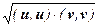+ (v, v) Û

Û (u , v) £ .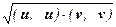

Последнее неравенство следует из неравенства Коши-Буняковского. (А почему справедлива первая эквивалентность в этой цепочке ?!).

Итак, в евклидовых пространствах можно оперировать с длинами, как в обычной геометрии на плоскости. Оказывается эта аналогия идёт ещё дальше: в евклидовом пространстве можно ввести понятие угла между векторами. Именно, пустьu, v – два ненулевых вектора евклидова пространства V . По неравенству Коши-Буняковского, 0 £ 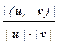£ 1. Поэтому существует однозначно определённый угол j Î [0, p],косинус которого равен 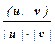. Назовем его углом между ненулевыми векторами uи v из векторного пространства V.

Понятие угла позволяет доказывать для произвольного евклидова пространства аналоги обычных теорем плоской геометрии. Например, аналог теоремы косинусов выглядит так:

Теорема (косинусов для евклидовых пространств). Пусть a, b –произвольные ненулевые элементы евклидова пространства V (аналоги смежных сторон треугольника). Тогда |a – b|² = |a|² + | b|² – 2×|a|×|b| cosj , где j – угол между векторами a , b.

Доказательство.По свойствам скалярного произведения и определению длин и угла, имеем:

|a – b|² = (a – b, a – b) = (a, a) – 2×(a, b) + (b, b) = |a|² + |b|² – 2×|a|×|b|×cosj .

Теорема доказана.

Упражнение. докажите аналоги теоремы Пифагора и теоремы синусов.