Свойства скалярного произведения

1⁰. скалярное произведение аддитивно по второму аргументу:

" u, v, wÎ V (u, v + w) = (u, v) + (u, w).

Действительно, используя свойства симметричности и аддитивности по первому аргументу, имеем:

(u, v + w) = (v+ w, u) = (v, u) + (w, u) = (u, v) + (u, w) .

2⁰.скалярное произведение однородно по второму аргументу:

" u, v Î V " a Î R (u, a×v) = a×(u, v).

Аналогично предыдущему, (u, a×v) = (a×v, u) = a×(u, v).

3⁰. " v Î V (v, 0) = (0, v) = 0 .

В самом деле, по свойству 2⁰, (v, 0) = (v, 0×0) = 0×(v, 0) = 0.

4⁰. скалярное произведение билинейно: " k, n Î N " u₁ , … , u_n , v₁ , … , v_k Î V

" a₁ , … , a_n , b₁ , … , b_k Î R .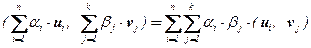

В самом деле, используя свойства аддитивности и однородности, имеем:

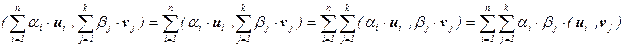
5⁰. Пусть V – конечномерное векторное пространство со скалярным произведением и базисом (e₁ , … , e_n ). Тогда скалярное произведение однозначно определяется значениями (e_i , e_j ) (1 £ £ n).

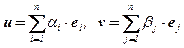Если , то 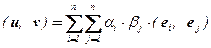. Таким образом, скалярное произведение векторовu, v Î Vполностью определяется их координатами a_i , b _j и указанными скалярными произведениями базисных векторов.

6⁰. Если V – конечномерное векторное пространство со скалярным произведением и базисом e = (e₁ , … , e_n), где (e_i , e_j) = 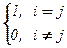, то " u, v Î V (u, v) = [u]_e [v]_e (напомним, что [x]_e – координатная строка вектора x Î V в базисе e).

Если 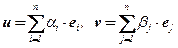, то .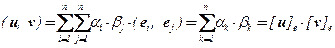

Любая упорядоченная пара (V, (_, _)), где V – векторное пространство, а (_, _) – скалярное произведение на V , называется евклидовым пространством. Необходимость такого формализма вызвана тем, что скалярное произведение на V можно задать по-разному. Поэтому, например,

(R², (u, v) = x₁×y₁ + 2×x₂×y₂) ¹ (R², (u, v) = x₁×y₁ + x₂×y₂).

Евклидово пространство (Rⁿ, (u, v) = x₁×y₁ + … + x_n×y_n) называется стандартным n-мерным евклидовым пространством, а скалярное произведение, заданное в нём – стандартным скалярным произведением в Rⁿ.