Мощности континуума
10. В любом бесконечном множестве M можно так выбрать счётное подмножество A Í M, что |M| = |M \ A|.
Будем рассуждать примерно так же, как ранее при доказательстве факта существования в бесконечном множестве бесконечной последовательности различных элементов (т.е. существования в бесконечном множестве счётного подмножества).
Выберем в M элемент a1 Î M и заметим, что M \ {a1} ¹ Æ. Значит можно выбрать b1 Î M \ {a1} и заметить, что M1 = M \ {a1 , b1} ¹ Æ. Если уже построены попарно различные элементы a1 , … , ak , b1 , … , bk Î M со свойством Mk = M \ {a1 , … , ak , b1 , … , bk } ¹ Æ, то в Mk выберем элемент ak+1 , а затем выберем bk+1 в Mk \ {ak+1} и снова получим
Mk+1 = M \ {a1 , … , ak , ak+1 , b1 , … , bk , bk+1 } ¹ Æ (?!).
 Таким образом, во множестве M выделено два счётных подмножества A = {a1 , a2 , … } и B = {b1 , b2 , … }. Зачем множество B ? С его помощью докажем, что |M \ A| = |M|. Для этого зададим отображение f : M ® M \ A следующим образом: f(x) =
Таким образом, во множестве M выделено два счётных подмножества A = {a1 , a2 , … } и B = {b1 , b2 , … }. Зачем множество B ? С его помощью докажем, что |M \ A| = |M|. Для этого зададим отображение f : M ® M \ A следующим образом: f(x) = 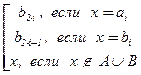 .
.
Легко понять что получится биективное отображение.
20. Всякое бесконечное подмножество счётного множества само счётно.
Пусть множество А счётно, B Í A. Тогда A = {а1 , а2 , ... , an , … }. Пусть 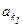 будет первым элементом этой последовательности, принадлежащим множеству В,
будет первым элементом этой последовательности, принадлежащим множеству В, 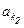 – вторым элементом с этим же свойством и т. д. Полагая
– вторым элементом с этим же свойством и т. д. Полагая 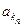 = bn , n Î N, получаем, что элементы подмножества В составляют последовательность b1 , b2 , ... , bn , ... , т.е. B счётно.
= bn , n Î N, получаем, что элементы подмножества В составляют последовательность b1 , b2 , ... , bn , ... , т.е. B счётно.
30. При добавлении конечной или счётной совокупности элементов к счётному множеству получается счётное множество.
Если к счётному множеству A = {a1 , a2 , ...} добавлено конечное множество B = {b1 , … , bk}, то взаимно-однозначное соответствие f: N ® A È B устанавливается формулой f(n) = 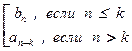 . Если же B = {b1 , b2 , … } – счётно, то f(n) =
. Если же B = {b1 , b2 , … } – счётно, то f(n) = 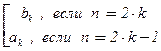 :
:

40. При добавлении конечной или счётной совокупности элементов к бесконечному множеству M получается равномощное ему множество K .
Действительно, в бесконечном множестве M выделим счётное подмножество A (см. рисунок ниже). Тогда для добавленного конечного или счётного множества K¢ = K \ M уже доказано, что |A È K¢| =À0 = |A|. Поэтому существует биекция j : A ® A È K, которая распространяется до биекции f: M ® M È K с помощью следующей формулы: f(m) = 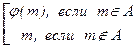 :
:
 |
50.Множество R всех действительных чисел равномощно любому отрезку (a; b), [a; b), (a; b], [a; b], т.е.
|(a; b)| = |[a; b)| = |(a; b]| = |[a; b]| = |R| = c.
Биективноесоответствие f : (a; b) ® R устанавливается школьной функцией f(x) = tg 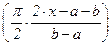 . Равномощность перечисленных отрезков следует из свойства 40.
. Равномощность перечисленных отрезков следует из свойства 40.
60. Если объединение счётного семейства конечных множеств бесконечно, то оно счётно. В частности, счётным является объединение счётного семейства попарно непересекающихся конечных множеств.
В самом деле, пусть даны конечные множества А1 , А2 , ... , Аn , ... и пусть их объединением будет множество В. Пронумеруем сначала все элементы конечного множества А1 , затем продолжим эту нумерацию, занумеровав все элементы множества А2 , и т.д. В итоге будут перенумерованы все элементы множества B, причём процесс нумерации не может закончиться на конечном шаге (иначе множество B было бы конечным). Значит, каждое натуральное число будет номером некоторого элемента из В, что и требовалось доказать.
Замечание: Условие на пересечение множеств существенно: если взять все множества равными, то получится конечное, а не счётное множество. Однако можно утверждать, что если объединение счётного семейства конечных множеств бесконечно, то это объединение счётно.
70. Объединение конечного или счётного семейства счётных множеств есть счётное множество.
Пусть даны счётные множества Ai = {ai1 , ai2 , …} (i Î Nили i Î {1, … , k}). Расположим их элементы в виде бесконечной прямоугольной таблицы одного из приведённых ниже видов: слева таблица для счётного семейства множеств, а справа – для конечного. Эти таблицы будем обходить в предписанном порядке (номера клеток написаны ниже самих элементов). На каждом шаге каждому ещё не пронумерованному элементу присвоим очередной номер.
| a11 | a12 | a13 | a14 | … | a11 | a12 | … | a1k k | ||
| a21 | a22 | a23 | a24 | … | a21 2×k | a22 2×k–1 | … | a2k k+1 | ||
| a31 | a32 | a33 | a34 | … | a31 2×k+1 | a32 2×k+2 | … | a3k 3×k | ||
| a41 | a42 | a43 | a44 | … | a41 4×k | a42 4×k–1 | … | a4k 3×k+1 | ||
| … | … | … | … | … | … | … | … | … |
Таким образом, в конечном итоге будут перенумерованы все элементы объединения рассматриваемого счётного или конечного семейства множеств.
80. Декартово произведение двух счётных множеств счётно.
В самом деле, пусть A = {a1 , a2 , … } и B = {b1 , b2 , … } – два счётных множества. Тогда A´B = {(a; b) | aÎ A Ù b Î B} = {(ai ; bj) | i, j Î N}, и пересчёт элементов этого множества можно осуществить так же, как и при доказательстве предыдущего свойства: вместо aij нужно рассматривать пару (ai ; bj ).
90. Декартово произведение любого конечного семейства счётных множеств счётно.
Пусть A1 , … , An – счётные множества. Тогда счётность декартова произведения можно доказать индукцией по n Î N: база имеется при n = 2, а индукционный переход обеспечивается формулой A1´ … ´ An = (A1 ´ … ´ An–1 ) ´ An .
100. Декартов квадрат [0; 1]´[0; 1] = {(a; b) Î R´R | a, b Î [0; 1]} равномощен отрезку [0; 1], т.е. |[0; 1]´[0; 1]| = c = |[0; 1]|.
Нужно установить биекцию f : [0; 1] ® [0; 1]´[0; 1] , однако сделать это непосредственно не так-то просто. Поэтому привлечём новые идеи о сравнении мощностей, которые строго будут обоснованы в следующем параграфе. Вначале докажем, что |[0; 1]| £ |[0; 1]´[0; 1]|, построив вложение (инъекцию) g : [0; 1] ® [0; 1]´[0; 1], а затем, вложив декартов квадрат в отрезок, докажем и обратное неравенство |[0; 1]´[0; 1]| £ |[0; 1]|. Из двух полученных неравенств будет следовать искомое равенство мощностей.
Ясно, что |[0; 1]| £ |[0; 1]´[0; 1]|, т.к. существует много инъективных отображений g : [0; 1] ® [0; 1]´[0; 1], например, заданное правилом g(x) = (x; 0).
Для доказательства обратного неравенства |[0; 1]´[0; 1]| £ |[0; 1]| построим инъективное отображение f : [0; 1]´[0; 1] ® [0; 1], используя десятичную запись действительных чисел: для a = 0, a1a2 … , b = 0, b1b2 … Î [0; 1] зададим значение f((a; b)) = g Î [0; 1], где g = 0, a1b1a2b2 … anbn … , т.е. в десятичной записи числа g цифры числа a поставим на нечётные места, а цифры числа b – на чётные места. При этом в качестве десятичного представления числа 1 (и только для него) будем рассматривать запись 0, 999… с бесконечным “хвостом” девяток. Тогда у числа g представление с бесконечным “хвостом” девяток может получиться только в случае наличия таких “хвостов” у a и у b, т.е при a = 1 = 0,999… = b и g = 0, 999…= 1 . Ясно, что f – отображение.
Оно инъективно: если f((a; b)) = f((e; d)), где e = 0, e1e2 … и d = 0, d1d2 … , то 0, a1b1a2b2 … = f((a; b)) = f((e; d)) = 0, e1d1e2d2 … , и an = en и bn = dn при любом n Î N (подробно разберите все возникающие случаи !!). Поэтому a = e, b = d и (a; b) = (e; d).
Таким образом, доказаны неравенства
|[0; 1]| £ |[0; 1]´[0; 1]| и |[0; 1]´[0; 1] | £ |[0; 1]| ,
из которых следует (пока интуитино), что |[0; 1]| = с = |[0; 1]´[0; 1]|.
Замечание: построеноое отображение f: [0; 1]´[0; 1] ® [0; 1] не сюръективно, т.к. у числа g = 0,1119 … 19 … = 0,11(19) Î [0; 1] нет прообраза: если a = 0,a1a2 … , b = 0,b1b2 … и f((a; b)) = g, то a = 0,111… = 0,(1), b = 0,199…9… = 0,20…, но
f((a; b)) = 0,12101010…10… = 0,12(10) ¹ 0,11(19) = g
– противоречие.
110. Если |A| = |B| , |C| = |D| , то |A´B| = |C´D|.В частности, декартово произведение R´R равномощно R, т.е. имеет мощность континуума: |R´R| = c = |R|.
Биекция f : A´B ® C´D задаётся правилом f((a; b)) = ((g(a); h(b))) Î C´D, где g : A ® C и h : B ® D – биекции.
Второе утверждение следует из того, что |R| = |[0; 1]| и предыдущего свойства.
Теперь легко понять, что |C| = с = |R|. Учитывая, что |R| = |R´R|, докажем, что |C| = |R´R|. Взаимно однозначное соответствие f : С® R´R устанавливается очевидным образом: f(a+i×b) = (a; b) Î R´R.
Таким образом, проведённое в этом параграфе исследование мощностей показало, что À0 = |N| = |Z| = |Q| < |R| = |C| = c.
Применим полученные результаты для решения старого и важного вопроса XIX в. о существовании трансцендентных чисел.
Действительное (или комплексное число) a называется алгебраическим, если оно является корнем некоторого многочлена f(x) с целыми коэффициентами. Множество всех многочленов с целыми коэффициентами обычно обозначается так:
Z[x] = { f(x) = an×xn+an–1×xn–1+…+a1×x+a0 | n Î N È {0} Ù ai Î Z(0 £ i £ n)}.
Поэтому можно записать
АR = {a Î R | $ f(x) Î Z[x] f(a) = 0}, АС= {a Î С | $ f(x) Î Z[x] f(a) = 0}
для множеств всех действительных и комплексных алгебраических чисел соответственно. Ясно, что AR Í AC.
Если действительное (или комплексное число) не является алгебраическим, т.е. оно не является корнем никакого многочлена f(x) с целыми коэффициентами, то такое число называется действительным (или комплексным) трансцендентным. Таким образом, множества TRи TC всех действительных (или комплексных) трансцендентных чисел можно задать так: TR = R \ АRи TС = С \ АС. Ясно, что TR Í TC .
С алгебраическими числами все давно знакомы:
Примеры: 1. Любое рациональное число a = 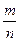 Î Q является алгебраическим, т.к. удовлетворяет уравнению n×x – m = 0 с целыми коэффициентами (f(x) = n×x – m). Таким образом, Q Í AR Í AC.
Î Q является алгебраическим, т.к. удовлетворяет уравнению n×x – m = 0 с целыми коэффициентами (f(x) = n×x – m). Таким образом, Q Í AR Í AC.
2. 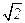 Î AR , т.к. является корнем многочлена f(x) = x2 – 2 с целыми коэффициентами.
Î AR , т.к. является корнем многочлена f(x) = x2 – 2 с целыми коэффициентами.
3. a = 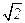 – i Î AC , т.к. a2 = 2 – 2×i×
– i Î AC , т.к. a2 = 2 – 2×i× 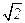 – 1 = 1 – 2×i×
– 1 = 1 – 2×i× 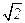 и (a – 1)2 = –8. Таким образом, a является корнем многочлена f(x) = (x–1)2 + 8 = x2 – 2×x + 9 с целыми коэффициентами.
и (a – 1)2 = –8. Таким образом, a является корнем многочлена f(x) = (x–1)2 + 8 = x2 – 2×x + 9 с целыми коэффициентами.
4. a = 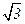 –
– 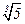 Î AR. Поиск аннулирующего это число многочлена аналогичен предыдущему примеру:
Î AR. Поиск аннулирующего это число многочлена аналогичен предыдущему примеру:
(a – 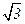 )3 = – 5, a3 – 3×
)3 = – 5, a3 – 3× 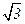 ×a2 + 9×a – 3×
×a2 + 9×a – 3× 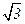 = –5, a3 + 9×a + 5 = 3×
= –5, a3 + 9×a + 5 = 3× 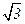 ×(a2 + 1),
×(a2 + 1),
(a3 + 9×a + 5)2 = 27×(a2 + 1)2, a6 + 81×a2 + 25 + 18×a4 + 10×a3 + 90×a = 27×(a4 + 2×a2 + 1),
a6 – 9×a4 + 10×a3 + 27×a2 + 90×a – 2 = 0.
Значит, a – корень многочлена f(x) = x6 – 9×x4 + 10×x3 + 27×x2 + 90×x – 2 Î Z[x].
5. Оказывается, что (AR , +, × ) и (AС , +, × ) – поля относительно обычных операций сложения и умножения действительных и комплексных чисел. Более того, поле AC алгебраически замкнуто, т.е. если a Î С является корнем многочлена bn×xn + … + b1×x + b0 с алгебраическими коэффициентами bn , … , b0 Î AC , то a Î AC . Эти нетривиальные результаты доказываются в курсе алгебры. Из них следует, что сколь угодно сложное выражение, полученное из алгебраических чисел с помощью операций сложения, умножения, деления, извлечения корней будет представлять алгебраическое число. Например, алгебраическим будет число
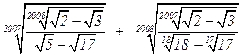 .
.
Таким образом, множества алгебраических чисел значительно богаче множества рациональных чисел. Этого нельзя сказать о трансцендентных числах: долгое время не было известно ни одного трансцендентного числа. Оказывается, что их существование можно доказать, используя теорию мощностей множеств.
Теорема (о счётности Z[x]). |Z[x]| = À0 .
Доказательство.Представим бесконечное множество M = Z[x]в виде объединения счётного семейства счётных множеств: M = 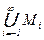 .
.
Положим Mi = {f(x) Î Z[x] | d(f) = i} – множество многочленов степени i. При этом M–1 = {0}, M0 = {f(x) = a0 ¹ 0 | a0 Î Z}, так что M–1 È M0 = Z . Для доказательства, что каждое Mi счётно представим Mi = 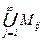 в виде объединения конечных множеств, где
в виде объединения конечных множеств, где
Mij = {f(x) = ai×xi+…+a1×x+a0 Î Mi | |ai|+…+|a0| = j}.
Чтобы понять, что каждое множество Mij конечно, заметим, что
|Mij| = |{(ai ; … ; a0 ) Î 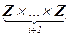 | |ai|+…+|a0| = j } |,
| |ai|+…+|a0| = j } |,
т.к. отображение l: Mij ® {(ai ; … ; a0 ) Î 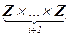 | |ai|+…+|a0| = j }, заданное правилом l(ai×xi+…+a1×x+a0) = (ai ; … ; a0 ), очевидно, биективно. Остаётся доказать конечность последнего множества: из равенства |ai|+…+|a0| = j следует, что |ak| £ j (k = 0, 1, … , i), т.е. ak Î {–j, –j+1, … , –1, 0, 1, … , j–1, j} может принимать не более 2×j+1 значения при каждом k = 0, … , i, а значит, |{(ai ; … ; a0 ) Î
| |ai|+…+|a0| = j }, заданное правилом l(ai×xi+…+a1×x+a0) = (ai ; … ; a0 ), очевидно, биективно. Остаётся доказать конечность последнего множества: из равенства |ai|+…+|a0| = j следует, что |ak| £ j (k = 0, 1, … , i), т.е. ak Î {–j, –j+1, … , –1, 0, 1, … , j–1, j} может принимать не более 2×j+1 значения при каждом k = 0, … , i, а значит, |{(ai ; … ; a0 ) Î 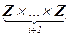 | |ai|+…+|a0| = j }| £ (2×j+1)i+1, что и требовалось.
| |ai|+…+|a0| = j }| £ (2×j+1)i+1, что и требовалось.
Теорема доказана.
Теорема (о счётности множеств алгебраических чисел).|AR| = À0 = |AC|.
Доказательство. Счётность множеств ARи AC доказывается единообразно: каждое из этих бесконечных множеств представляется в виде счётного объединения конечных множеств.
Для этого воспользуемся следующим известным из курса алгебры утверждением: многочлен f(x) степени n с комплексными коэффициентами имеет не более n корней. Другими словами, если Kf = {a Î C | f(a) = 0} – множество корней многочлена f(x), то |Kf| £ n.
Если рассмотреть теперь множество K = 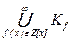 , то оно счётно (т.к. Z[x] счётно) и состоит из всех корней многочленов с целыми коэффициентами, т.е. совпадает с AC . Таким образом, доказано, что множество AC счётно.
, то оно счётно (т.к. Z[x] счётно) и состоит из всех корней многочленов с целыми коэффициентами, т.е. совпадает с AC . Таким образом, доказано, что множество AC счётно.
Если в проведённом рассуждении положить Kf = {a Î R | f(a) = 0}, то получим счётность множества AR .
Теорема доказана.
Теорема (Кантора о существовании трансцендентных чисел). Существуют трансцендентные числа.
Доказательство.Поскольку R несчётно, а AR счётно, то TR =R \ AR ¹ Æ.
Теорема доказана.
Таким образом, теория множеств привела к получению нетривиального результата теории чисел. На самом деле множество трансцендентных чисел TR (а значит, и TC) несчётно: если бы TR было конечно или счётно, то множество R = AR È TR было бы счётно, а это не так. Тем более удивительно, что конкретные примеры трансцендентных чисел долго не удавалось найти. Первые такие примеры были построены Ж. Лиувиллем в середине XIX в., а в конце этого века было доказано, что трансцендентны известные математические константы e и p (теоремы Ш. Эрмита и К. Линдемана).
Дата добавления: 2021-12-14; просмотров: 518;











