Резонанс напряжений

Если последовательно с генератором соединить конденсатор и катушку индуктивности, то, при условии равенства их реактивных сопротивлений, возникнет резонанс напряжений. При этом активная часть Z должно быть как можно меньшей.

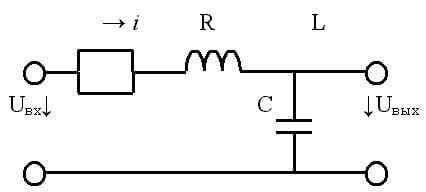
Стоит отметить, что индуктивность и емкость обладает только реактивными качествами лишь в идеализированных примерах. В реальных же цепях и элементах всегда присутствует активное сопротивление проводников, хоть оно и крайне мало.

При резонансе происходит обмен энергией между дросселем и конденсатором. В идеальных примерах при первоначальном подключении источника энергии (генератора) энергия накапливается в конденсаторе (или дросселе) и после его отключения происходят незатухающие колебания за счет этого обмена.

Напряжения на индуктивности и емкости примерно одинаковы, согласно закону Ома: U=I/X. Где X — это Xc емкостное или XL индуктивное сопротивление соответственно.

Цепь, состоящую из индуктивности и емкости, называют колебательным контуром. Его частота вычисляется по формуле: Период колебаний определяется по формуле Томпсона:

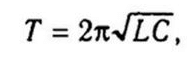
Так как реактивное сопротивление зависит от частоты, то сопротивление индуктивности с ростом частоты увеличивается, а у ёмкости падает. Когда сопротивления равны, то общее сопротивление сильно снижается, что отражено на графике:

Основными характеристиками контура являются добротность (Q) и частота. Если рассмотреть контур в качестве четырехполюсника, то его коэффициент передачи после несложных вычислений сводится к добротности: K=Q

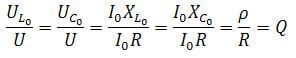
А напряжение на выводах цепи увеличивается пропорционально коэффициенту передачи (добротности) контура. Uк=Uвх*Q

При резонансе напряжений, чем выше добротность, тем больше напряжение на элементах контура будет превышать напряжение подключенного генератора. Напряжение может повышаться в десятки и сотни раз. Это отображено на графике:

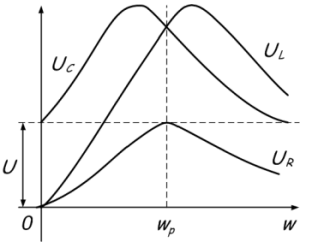
Потери мощности в контуре обусловлены только наличием активного сопротивления. Энергия из источника питания берется только для поддержания колебаний.

Коэффициент мощности будет равен: cosФ=1. Эта формула показывает, что потери происходят за счет активной мощности: S=P/Cosф

Резонанс токов

Резонанс токов наблюдается в цепях, где индуктивность и емкость соединены параллельно.

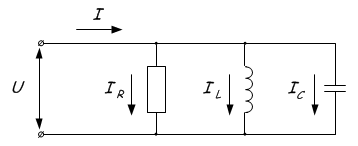
Явление заключается в протекании токов большой величины между конденсатором и катушкой, при нулевом токе в неразветвленной части цепи. Это объясняется тем, что при достижении резонансной частоты общее сопротивление Z возрастает. Или простым языком звучит так – в точке резонанса достигается максимальное общее значение сопротивления Z, после чего одно из сопротивлений увеличивается, а другое снижается в зависимости от того растет или снижается частота. Это наглядно отображено на графике:

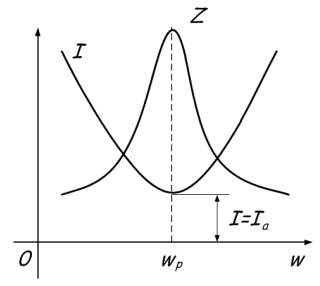
В общем, всё аналогично предыдущему явлению, условия возникновения резонанса токов следующие:

1.Частота питания аналогична резонансной у контура.

2.Проводимости у индуктивности и ёмкости по переменному току равны BL=Bc, B=1/X.