Внешняя устойчивость резонансов в динамических системах

Исследованию устойчивости движения по Ляпунову посвящается значительное количество научных трудов. Вопросы исследования устойчивости резонансов в системах с быстрыми и медленными переменными при действии возмущений также рассматриваются в широком круге работ. Как правило, в работах под устойчивостью резонансов понималась устойчивость решений системы внутри асимптотически малой резонансной зоны. В то же время резонансы могут определять эволюцию медленных переменных уже на нерезонансных участках движения. Подобные явления, известные как вторичные резонансные эффекты, наблюдаются при усреднении систем с медленной эволюцией на нерезонансных участках движения. При этом, в усредненных уравнениях резонансные знаменатели входят в члены второго приближения метода усреднения, поэтому влияние вторичных резонансных эффектов на изменение переменных является существенным при отсутствии эволюции в первом приближении. Усредняя медленно изменяющиеся переменные системы, можно получить условия внешней устойчивости резонанса в нерезонансном случае. Тогда, под внутренней устойчивостью следует понимать устойчивость решений в резонансном случае.

Остановимся подробнее на рассмотрении данных резонансных эффектов и внешней устойчивости резонансов. Садов Ю.А. исследовал вторичный резонансный эффект в почти гамильтоновой двухчастотной системе, уравнения которой имели вид [9]:

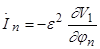, (1.78)

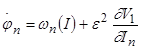, (1.79)

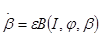, (1.80)

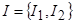где n=1,2; - угловые переменные (быстрые фазы с периодом 2p); - переменные действия (медленные переменные с периодом 2p); 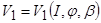- возмущенная часть гамильтониана, 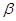-переменная, соответствующая дополнительной неконсервативной степени свободы.

Уравнения для медленных переменных (1.78) усредняется по быстрым переменным на нерезонансном участке движения с учетом действующих возмущений. В результате, изменение усредненных переменных описывается следующей системой уравнений:

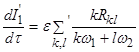, (1.81)

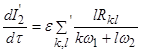. (1.82)

Здесь 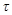- медленное время, 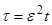, - некоторые функции усредненных переменных и . В выражениях (1.81)-(1.82) штрих при знаке суммирования означает отсутствие члена с k=l=0. При получении уравнений (1.81)-(1.82), число членов в разложении возмущающих функций в ряд Фурье, предполагается конечным ( 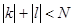). «Это позволяет отвлечься от не относящихся к делу сложностей, связанных с плотным множеством резонансов.» Как это следует из уравнений (1.60)-(1.61), усреднение по быстрым фазам приводит к равенству нулю членов метода усреднения, соответствующих k=l=0. Это вызвано тем, что учитываемые возмущающие функции являются периодическими со средним значением равным нулю. Характерной чертой выражений (4)-(5) является наличие в их знаменателях частот, обращающихся в ноль на резонансной поверхности. Влияние этих членов на изменение медленных переменных Садов Ю.А. определил как вторичный резонансный эффект. Поскольку, уравнения (1.81)-(1.82) получены на нерезонансных участках движения, то вторичный резонансный эффект проявляется лишь вне конечного числа резонансных зон. Данный эффект имеет «амплитудное» происхождение и связан не с «расхождением траекторий, отличающихся сдвигом фаз, а с (медленным) увеличением амплитуд колебаний медленных переменных системы вблизи резонанса. В этом смысле проявляющиеся здесь резонансные эффекты имеют вторичный, наведенный характер». Наиболее очевидным результатом влияния вторичного резонансного эффекта является «увеличение скорости эволюции при приближении к резонансам», так как в этом случае знаменатели членов второго приближения стремятся к нулю. При естественном введении диссипативных факторов в систему (уравнение (1.80)) движение по быстрой «негамильтоновой» переменной 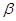задемпфировано. По этой причине эта переменная приближается к одному из устойчивых положений равновесия и затем постоянно остается вблизи этого положения с точностью до величин порядка e. Ю.А.Садовым показывается, что вторичный резонанс не наблюдается при изменении невозмущенной части гамильтониана, построенной по усредненным переменным.

В дальнейшем [9], [10] Ю.А. Садов переходит к исследованию многочастотных механических систем и показывает, что вторичные резонансные эффекты возможны в таких системах. Кроме того, им вводятся понятия внешней (в силу нерезонансных уравнений) и внутренней (в силу резонансных уравнений) устойчивости резонансов.

Изучаемые многочастотные системы записываются в стандартной форме [9]:

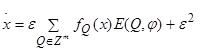, (1.83)

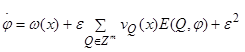, (1.84)

где 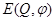= , , 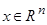, x - n векторных переменных; 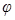- m быстрых фаз, Q - m-мерный целочисленный вектор, определяющий гармонику тригонометрических рядов:

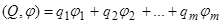. (1.85)

Для исключения быстрых фаз 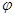из уравнений (1.83)-(1.84) вводится усредняющая замена переменных:

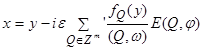. (1.86)

Усредненные таким образом уравнения для медленных переменных принимают вид:

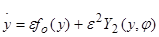, (1.87)

где .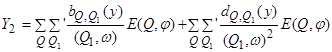

Вторичные резонансные эффекты обусловлены влиянием резонансных членов в знаменателях второго приближения уравнения (1.87) пропорциональных 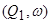. Данные члены определяют эволюцию медленных переменных в вырожденном случае на временах .

Рассматривается случай одной медленной переменной n=1. В этом случае имеется единственное уравнение (1.87), причем, 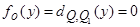. Фазовым пространством системы является прямая линия, а резонансам соответствуют дискретно расположенные на этой прямой точки. Из вида уравнения следует, что если точка 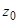соответствует резонансу =0, то существует (при условии 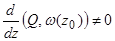) конечная окрестность, в которой правая часть уравнения принимает с разных сторон от резонансной точки значения разных знаков. Эти значения уходят в бесконечность при приближении к резонансу. Следовательно, каждая точка из данной окрестности притягивается к резонансу при условии , или выталкивается из окрестности, в случае противоположного знака этого неравенства.

Наличие околорезонансных стационарных точек можно пояснить следующим образом: если между двумя соседними резонансами выражение 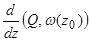не изменяет своего знака, то правая часть усредненного уравнения изменяется от -¥ до +¥, поэтому между резонансами найдется точка, имеющая нулевое значение правой части. Причём, можно показать, что если система имеет бесконечно много дискретно расположенных резонансов и правые части исходных уравнений гладкие, то расстояние между такой нерезонансной точкой и соответствующим резонансом стремится к нулю при стремлении порядка резонанса к бесконечности. Поэтому, такие точки названы околорезонансными стационарными точками.

Указанные результаты справедливы вне резонансных зон асимптотически малой ширины. Внутри данных зон для получения усредненных решений используется схема усреднения, принципиально отличная от нерезонансной схемы. В силу этих уравнений резонансная зона может являться устойчивым или неустойчивым множеством. Причём, знак этой устойчивости, в общем случае, не зависит от устойчивости резонансной зоны по нерезонансным усредненным уравнениям. По этой причине, предполагается различать внешнюю устойчивость резонансов по нерезонансным усредненным уравнениям за счет влияния вторичных резонансных эффектов вне малой резонансной зоны и внутреннюю устойчивость резонансов, согласно резонансным усредненным уравнениям внутри резонансной зоны.

Случай нескольких медленных переменных отличается от одномерного случая тем, что каждое резонансное множество представляет собой не точку, а в общем случае n-1 - мерное многообразие. При внешней устойчивости резонанса траектории стремятся к асимптотически малой окрестности данного многообразия. Согласно, терминологии Садова Ю.А. запишем уравнение движения по нормали к резонансному множеству в его малой окрестности:

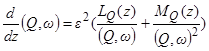. (1.88)

Важным следствием уравнения (1.88) является тот факт, что второе слагаемое в его правой части всегда равно нулю: 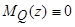. Поэтому, как и в одномерном случае, при нескольких медленных переменных, резонанс может быть либо внешне устойчивым (притягивающим) при условии или внешне неустойчивым (выталкивающим) в противоположном случае. Однако, при нескольких медленных переменных, указанное свойство уже не характеризует всё резонансное множество, так как в общем случае знак выражения (1.88) может быть разным для различных точек множества. Следовательно, в общем случае, можно говорить лишь о локальной внешней устойчивости резонанса. Второе следствие из уравнения (1.88) состоит в том, что, так как нет оснований полагать, что скорость движения в двух произвольных направлениях не содержит членов, обратно пропорциональных квадрату расстояния от резонанса, то скорость приближения к резонансу или удаления от него меньше, чем скорость движения вдоль резонансного множества.