Лабораторное занятие № 2 Разветвленная цепь переменного тока с катушкой индуктивности и конденсатором.
Цель работы: опытным путем проверить основные законы для цепи переменного тока с последовательным соединением приемников электрической энергии: резистора, катушки индуктивности и конденсатора.
Основные теоретические положения
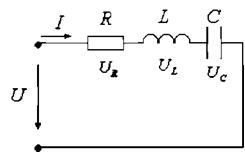
Если на вход электрической цепи с последовательно соединенными активным сопротивлением R, индуктивностью L и емкостью С подается переменное синусоидальное напряжение 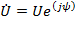
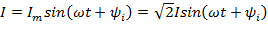
комплексное значение которого то по цепи будет протекать ток 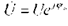 .
. 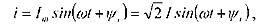 комплексное значение которого
комплексное значение которого 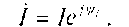
Согласно второму закону Кирхгофа в комплексной форме записи напряжение, подводимое к этой электрической цепи, может быть записано 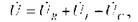 где
где 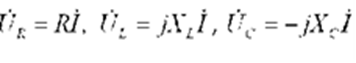 - комплексные напряжения на участках цепи.
- комплексные напряжения на участках цепи.
Причем 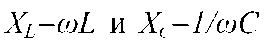 - индуктивное и емкостное сопротивления
- индуктивное и емкостное сопротивления 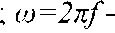 - угловая частота;/- частота напряжения.
- угловая частота;/- частота напряжения.
Если комплексы напряжений активного, индуктивного и емкостного участков цепи заменить произведениями комплексов тока и сопротивления, то уравнение для подводимого к электрической цепи комплексного напряжения преобразуется к виду
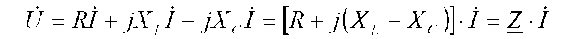
или к виду уравнения, записанного в комплексной форме по закону Ома для всей цепи: 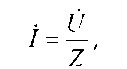 . Где
. Где 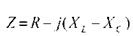 - полное комплексное сопротивление электрической цепи переменного тока.
- полное комплексное сопротивление электрической цепи переменного тока.
Модуль полного комплексного сопротивления цепи переменного тока 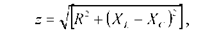 а аргумент
а аргумент 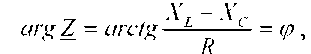
есть угол между векторами напряжения и тока, определяемый как разность начальных фаз соответственно 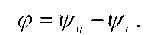
С учетом того, что на резисторе R напряжение совпадает по фазе с током 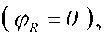 на индуктивности L напряжение опережает ток на угол
на индуктивности L напряжение опережает ток на угол 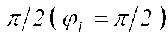 , а на емкости С напряжение отстает от тока на
, а на емкости С напряжение отстает от тока на 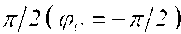 , построенная векторная диаграмма для электрической цепи представлена.
, построенная векторная диаграмма для электрической цепи представлена.

Взаимосвязь между действующими значениями тока и напряжения и полным сопротивлением цепи определяется соотношениями 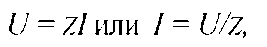 где действующие значения напряжения
где действующие значения напряжения 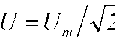 и тока
и тока 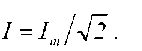
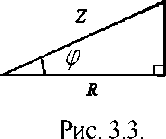
Из треугольника напряжений на векторной диаграмме, можно получить треугольник сопротивлений для рассматриваемой цепи, разделив стороны этого треугольника на комплексный ток /, из которого следует, что 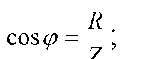 ,
, 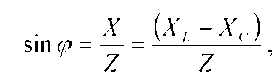 а также треугольник мощностей умножив стороны треугольника сопротивлений на квадрат тока в цепи .
а также треугольник мощностей умножив стороны треугольника сопротивлений на квадрат тока в цепи .
Активная мощность цепи переменного тока 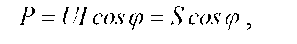 отсюда
отсюда 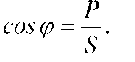
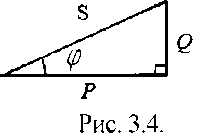
Из треугольника мощностей можно установить взаимосвязь между активной Р, полной S и реактивной Q мощностями электрической цепи:
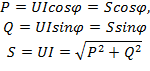
При этом реактивная составляющая полной мощности цепи находится как разность реактивной индуктивной 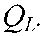 и реактивной емкостной составляющих
и реактивной емкостной составляющих 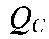 :
: 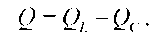
Выражения для полной мощности цепи переменного тока в комплексной форме записывают в следующем виде:
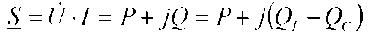 или
или 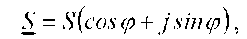
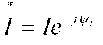 где - сопряженное значение комплексного тока
где - сопряженное значение комплексного тока 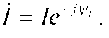
Полученные выражения показывают, что угол сдвига фаз между током I и напряжением U питающей сети зависит от характера сопротивлений, включенных в цепь переменного тока. При этом если
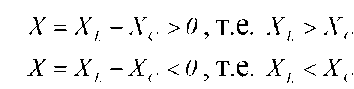
| характер нагрузки индуктивный, характер нагрузки емкостной. |
Однако возможно особое состояние цепи переменного тока при последовательном включении активного сопротивления R индуктивности L и емкости С, при котором индуктивное сопротивление цепи равно емкостному сопротивлению 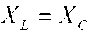 .
. 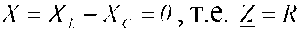 - характер нагрузки чисто активный.
- характер нагрузки чисто активный.
Это явление в неразветвленной электрической цепи переменного тока называется резонансом напряжений.
Условием для возникновения резонанса является равенство реактивных сопротивлений 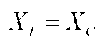 и равенство нулю разности фаз тока и напряжения на входе цепи
и равенство нулю разности фаз тока и напряжения на входе цепи 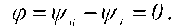 Частота, на которой возникнет равенство реактивных сопротивлений, называется резонансной и определяется как
Частота, на которой возникнет равенство реактивных сопротивлений, называется резонансной и определяется как 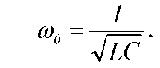
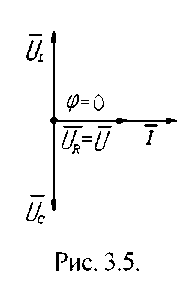
В простейшем случае резонанс напряжений может быть получен в электрической цепи при последовательном включении катушки индуктивности и конденсаторов за счет изменения емкости конденсаторов при постоянных параметрах катушки. Значения частоты, индуктивности, напряжения и активного сопротивления цепи неизменны. Векторная диаграмма тока и напряжений этой цепи при резонансе представлена на рис. 3.5.
Реактивная составляющая напряжения Uj.. на катушке при резонансе равна напряжению Ur на конденсаторе, напряжение источника U приложено к активному сопротивлению R. Точка резонанса в этих условиях определяется по наибольшему значению тока в электрической цепи.
Для резонанса напряжений характерно;
Полное сопротивление электрической цепи переменного тока минимально и равно ее активному сопротивлению, т.е.
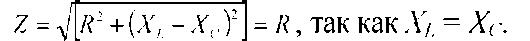
При неизменном напряжении питающей сети (U=consT) ток в цепи достигает наибольшего значения 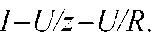
Коэффициент мощности 1 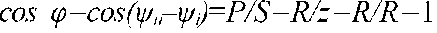 ^
^
максимальный, (соответствующий 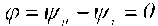 ). Это значит, что вектор тока / и вектор напряжения и сети совпадают по направлению, т.к. имеют равные начальные фазы
). Это значит, что вектор тока / и вектор напряжения и сети совпадают по направлению, т.к. имеют равные начальные фазы 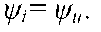
Активная мощность 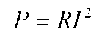 имеет наибольшее значение, равное
имеет наибольшее значение, равное
полной мощности 5, а реактивная мощность цепи 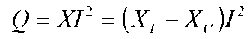 равна нулю
равна нулю 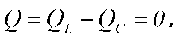
Однако реактивная индуктивная и реактивная емкостная составляющие полной мощности 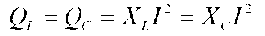 могут приобретать большие значения, в зависимости от значении тока и реактивных сопротивлений.
могут приобретать большие значения, в зависимости от значении тока и реактивных сопротивлений.
Напряжения на емкости и индуктивности равны
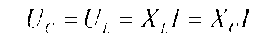 и в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети.
и в зависимости от тока и реактивных сопротивлений могут принимать большие значения, во много раз превышающие напряжение питающей сети.
Напряжение на активном сопротивлении равно напряжению питающей сети, т.е. 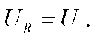
При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и перенапряжения на отдельных ее участках. Поэтому, резонанс напряжений в промышленных электротехнических установках нежелательное и опасное явление, т.к. может привести к аварии вследствие недопустимого перегрева отдельных элементов электрической цепи или к пробою изоляции обмоток электрических машин и аппаратов, изоляции кабелей и конденсаторов. В то же время резонанс напряжений широко используется в радиотехнике и электронике для выделения сигналов заданной частоты.
Методические указания по выполнению работы
1. Собрать на рабочем поле экрана электрическую цепь синусоидального тока с последовательным соединением резистора, катушки и конденсатора. Катушка индуктивности является реальной, поэтому она обладает активным сопротивленнем обмотки.

 Схема цепи с последовательным соединением резистора, катушки и конденсатора
Схема цепи с последовательным соединением резистора, катушки и конденсатора
|
Элементы электрической цепи берутся из окон выбора источников и компонентов. Измерительные приборы - с верхней панели индикаторов, осциллограф - из боковой панели инструментов.
Измерительные приборы (амперметр и вольтметр) необходимо переключить в режим измерения переменного тока АС.
Для соединения элементов схемы необходимо подвести курсор к подсоединяемому концу одного элемента до появления точки на конце этого элемента, нажать левую кнопку мыши, подвести линию - «провод» к началу следующего элемента до появления точки, снова нажать левую кнопку мыши.
2. Задать параметры элементов цепи согласно варианту .
| № варианта | |||||||
| Напряжение источника питания (U В | |||||||
| Частота напряжения источника питания (Гц) | |||||||
| Начальная фаза напряжения источника питания | |||||||
| Сопротивление резистора R, Ом | |||||||
| Индуктивность катушки Z, мГн | |||||||
| Активное сопротивление катушки индуктивности ТС, Ом | |||||||
| Емкость конденсатора С, мкФ |
Провод, идущий на канал «А» осциллографа, необходимо обозначить красным цветом, подведя курсор к проводу, и, нажав, правую кнопку мыши, затем «Color Segment», выбрать цвет (красный).
Включить цепь, нажав клавишу (  положениe «I») в правом верхнем углу монитора.
положениe «I») в правом верхнем углу монитора.
После появления показаний приборов выключить цепь, нажав ту же клавишу (положение «О»).
Для наблюдения осциллограмм напряжения и тока необходимо активизировать осциллограф двойным нажатием левой кнопки мыши.
Можно расширить осциллограф, растянув его по горизоитали и вертикали. В случае необходимости настроить осциллограф: горизонтальная развертка регулируется кнопками «Time base», при этом изображение сжимается или расширяется по горизонтали (по оси времени).
Масштаб синусоид устанавливается заданием цены деления по вертикальной оси «V/div» .
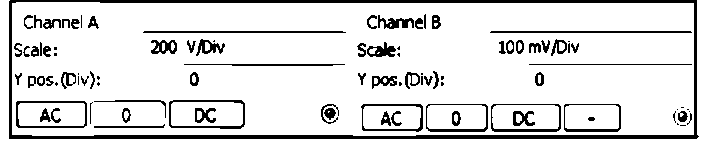
На канале «А» отображается синусоида напряжения (красная), на канале «В» - синусоида тока (черная).
С помощью осциллографа можно измерить угол сдвига фаз между напряжением и током цепи.
Для измерения угла сдвига фаз ср между напряжением и током необходимо подвести красный курсор к началу синусоиды напряжения (красная синусоида), а синий - к началу синусоиды тока (черная синусоида).
В правом окне осциллографа (рис. 3.9.) значение (Т2-Т1) необходимо перевести в градусы; 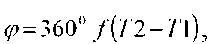

где f - частота напряжения источника питания, Гц.
Обязательно обратить внимание на знак угла φ.
3. Заполнить таблицу согласно снятым показаниям приборов . Рассчитать недостающие параметры.
| Элементы цепи | Измерен ные величины | Известные величины | Вычисленные значения | |||||||||
| U В | I А | R Ом | L Гн | С мкФ | Z | X | cos φ | φ | Q Вар | Р Вт | ||
| Ом | ||||||||||||
| Цепь в целом | ||||||||||||
| Резистор | ||||||||||||
| Катушка индуктивно сти | ||||||||||||
| Конденсатор |
Полное сопротивление цепи: 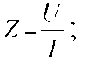 ,
, 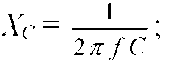
Индуктивное сопротивление катушки: 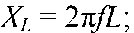 Емкостное сопротивление конденсатора:
Емкостное сопротивление конденсатора:
Из треугольника сопротивлений: 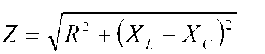
Коэффициент мощности: 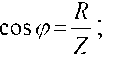
Угол сдвига фаз: 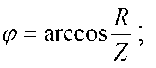
Из треугольника мощностей:
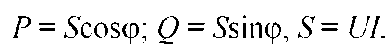
Дата добавления: 2021-12-14; просмотров: 514;











