Использование закона Ома и правила Кирхгофа для расчета электрических цепей переменного тока.

Переменный ток не имеет направления, однако для анализа и расчетов цепей переменного тока задаются условные направления токов в цепи и источников ЭДС. Тогда сложение и вычитание переменных токов, напряжений и ЭДС в схеме происходит с учетом этих направлений, что в свою очередь, позволяет применять при расчетах все законы постоянного тока.

Для расчёта токов, напряжений и других параметров ветви применяется закон Ома (в комплексной форме):

Комплексный ток (Д.

Комплексное сопротивление {2).

Комплексная проводимость (У).

Последовательное соединение элементов составляет не- разветвленную электрическую цепь. Ток, протекающий через эти элементы, один и тот же:

где Z_i— комплексное сопротивление пассивного элемента; U_i - комплексное падение напряжения на пассивном элементе.

Общее комплексное сопротивление ветви составляет:

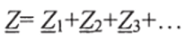
В схеме комплексные сопротивления ветвей

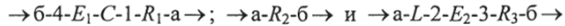соответственно равны:

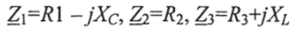
Если в последовательную цепь включены источники ЭДС, заданы направление тока в цепи и сопротивление отдельных элементов, то напряжение на участке цепи можно определить из обобщенного закона Ома для комплексных величин: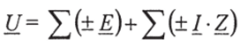

При вычисления U прежде всего задается (положительное) условное направление напряжения. Суммирование падений напряжения на отдельных элементах производится с учетом знаков:

ЭДС Е принимает знак " + " при совпадении условного обхода контура с положительным направлением источника ЭДС, в противном случае - знак

Ток / принимает знак "+" при совпадении условного обхода контура с направлением тока, в противном случае - знак«-»

В схеме в ветви -»б - 4-Е-С--Я~ а-> напряжение

Параллельное соединение элементов имеет только два узла, к которым подключены все ветви электрической цепи. Если к этим узлам приложено напряжение Ц, то ток в каждой ветви соответственно будет равен:

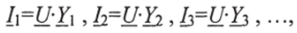
где Y,— комплексная проводимость ветви.

Общая проводимость параллельного соединения равна:

В схеме ветви ->б - 4 - Е₁ - С - - 1 - R₁ -a →, а ->R₂ - б-> и-»а -L - 2 - E₂ - 3 - R_з - б-»соединены параллельно. Соответственно комплексные проводимости ветвей будут равны:

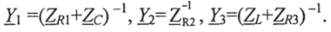
Для расчета токов в узле применяют первый закон Кирхгофа - алгебраическая сумма комплексных токов / в любом узле электрической цепи равна нулю:

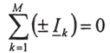
Со знаком "+" суммируются токи с условным направлением к узлу, а со знаком " - " токи с условным направлением от узла. Из первого закона Кирхгофа следует, что сумма комплексных токов, направленных к узлу, равна сумме комплексных токов, направленных от узла.

В схеме рис.2.41 сумма токов:

В узле "а" I1 - I2 - I3 = 0, в узле "б" - I1 +I2+I3 =0.

Для расчета токов и напряжений в замкнутом контуре применяют второй закон Кирхгофа в комплексной форме:

Алгебраическая сумма комплексных ЭДС (Е) в замкнутом контуре равна алгебраической сумме произведений комплексных значений тока (Г) на соответствующие комплексные значения полных сопротивлений и алгебраической сумме комплексных напряжений (Ц) в этом же контуре.

Знак «+» E, I или U принимает в случае совпадения с условным направлением обхода контура, в противном случае Е, I или U принимает знак « - ».

Второй закон Кирхгофа применим только к одному контуру, поэтому для многоконтурной электрической цепи необходимо выделить независимые контуры, задать условные направления токов, напряжений и ЭДС, выбрать условное направление обхода контуров и учесть влияние смежных контуров. Для электрической схемы :

а) Контур б-4-E1-С-1-R1-а-R2-б получаем, исключив из схемы ветвь a→ L- 2 - Е₂ -3 - Rз — б→ . Для этого контура при обходе в направлении тока |ц второй закон Кирхгофа:

б) Контур &-Ь-2-Ег-Ъ -Яг- 6-Яг- л получаем, исключив из схемы ветвь ->б - 4-Е-С--Я- а—>. Для этого контура при обходе в направлении тока /22 второй закон Кирхгофа: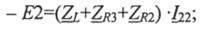

в) Если рассматривать эти два контура совместно, то для контура б-4-E₁-С-1-R₁-а-R₂-б необходимо учитывать ток I₂₁, направление которого противоположно току I₁₁(направлению обхода),

а для контура а-L-2-E₂-3-Rз-б-R₂- а необходимо учитывать ток /и, направление которого противоположно току I₂₂ (направлению обхода)