Емкость в цепи переменного тока

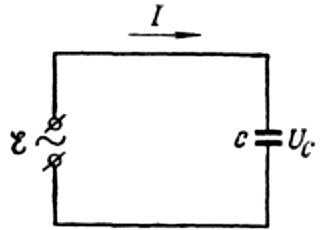
Рассмотрим электрическую цепь, которая состоит только из источника переменного тока и конденсатора . Как известно, конденсатор (две металлические пластины, между которыми – диэлектрик) вообще не пропускает постоянный ток (ток будет протекать только до тех пор, пока конденсатор заряжается, а потом исчезает). Но если на конденсатор подавать переменное напряжение, он все время будет перезаряжаться, то есть через конденсатор может идти переменный ток . 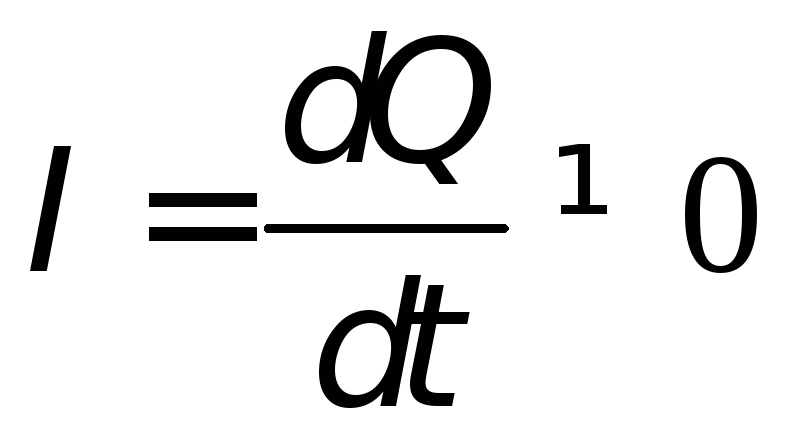Чем больше частота переменного тока и емкость конденсатора, тем лучше он пропускает ток, тем меньшим будет его емкостное сопротивление. Найдем это сопротивление, то есть сопротивление, которое создает конденсатор переменному току.

Пусть через конденсатор течет ток, который меняется по закону (1) 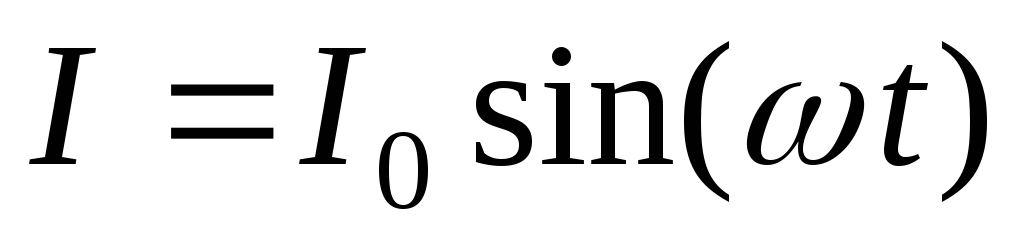. Из определения силы тока 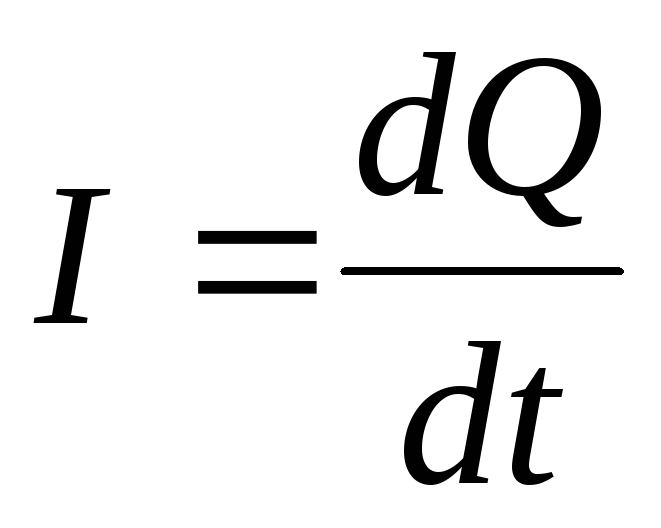, можно найти заряд на обкладках конденсатора: , .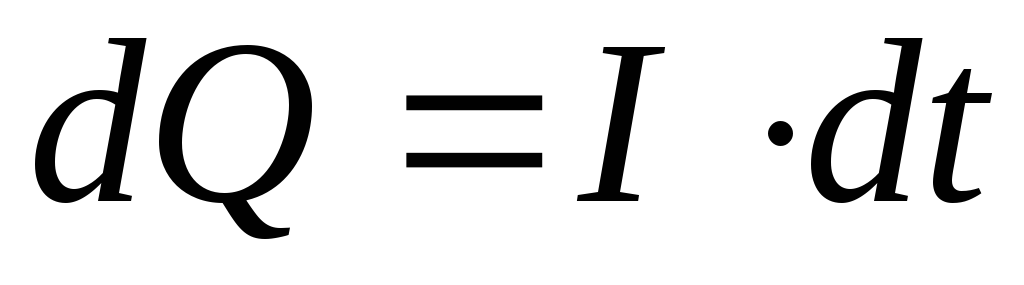

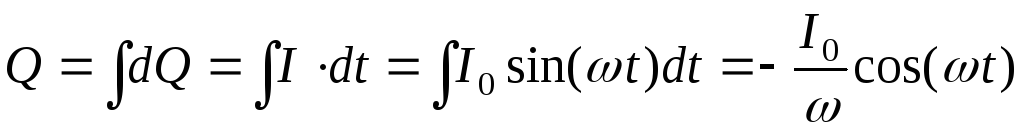Учитывая, что , получаем 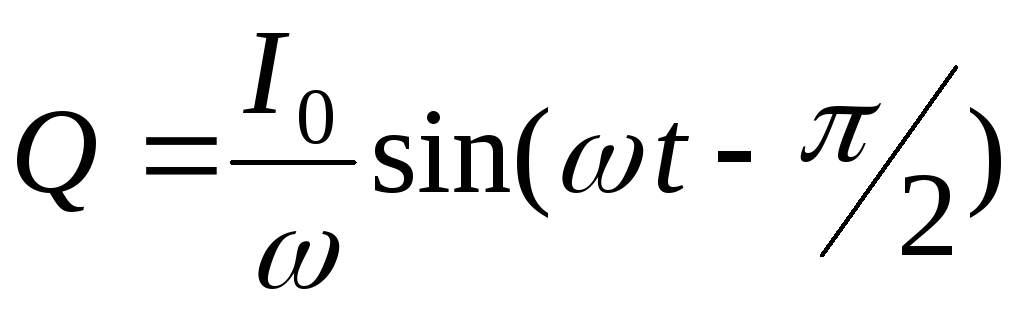. Из определения электроемкости конденсатора 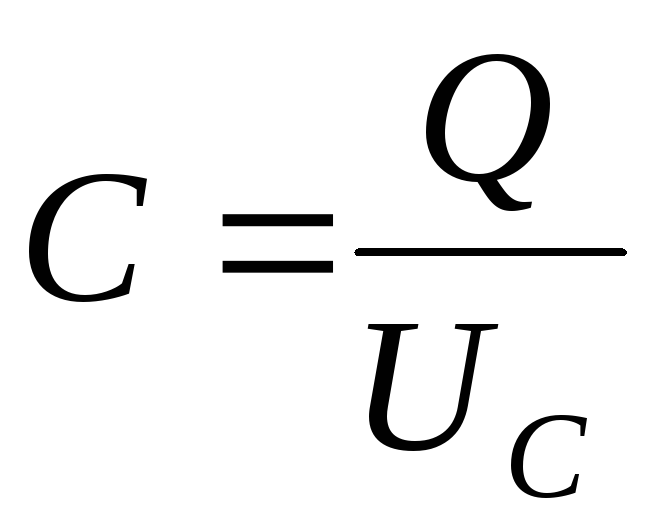, вытекает, что напряжение на его обкладках будет .

Величина 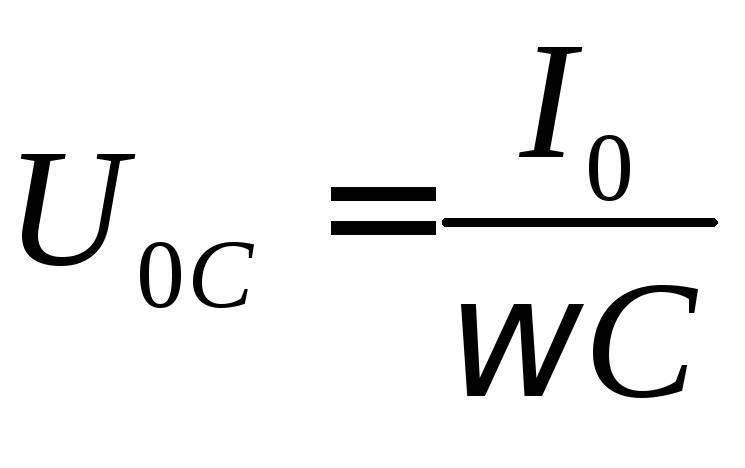является амплитудным значением напряжения на емкости, а отношение называют емкостным сопротивлением. На емкостном сопротивлении, как и на индуктивном, джоулево тепло не выделяется. Анализируя это выражение, можно сделать вывод, что конденсатор хорошо пропускает переменный ток высокой частоты и хуже пропускает ток малой частоты.

Из сравнения выражений для тока и напряжения на конденсаторе вытекает, что колебания напряжения на конденсаторе отстают от колебаний тока на 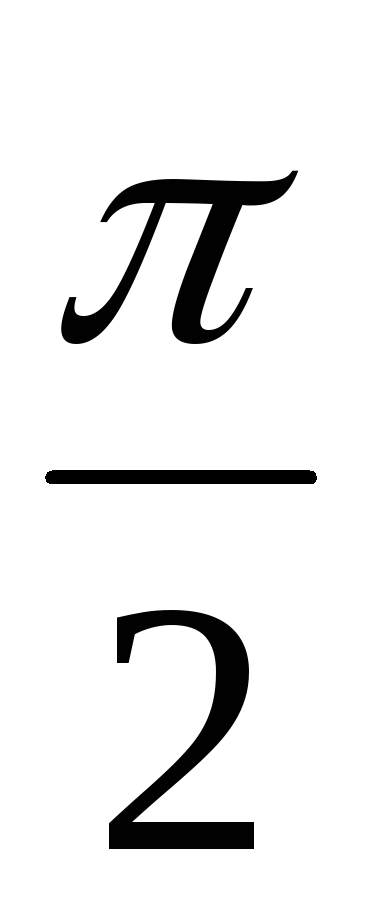. То есть сначала через конденсатор протекает ток (конденсатор заряжается), а уже потом на нем возникает напряжение. Когда ток достигает максимального значения – напряжение на конденсаторе равняется нулю, и наоборот, когда напряжение максимальное – ток равняется нулю.