Интерпретации формул исчисления предикатов

Уже в исчислении высказываний возникала ситуация, когда было невозможно однозначно говорить об истинности или ложности формулы: при одних значениях пропозициональных переменных эта формула может принимать значение истина, а при других – ложь. Только значения тождественно истинных или тождественно ложных формул не зависят от выбора набора значений их переменных. Таким образом, судить об истинности формулы исчисления высказываний можно, только фиксировав те или иные значения её переменных, т.е. выбрав ту или иную интерпретацию.

Ещё сложнее обстоит дело с формулами исчисления предикатов. Если рассмотреть какую-либо формулу исчисления предикатов, например, ($ x P(x, y)), то P(x, y) является не более чем символом, лишённым всякого содержания. Как отмечалось выше, географ может подставить вместо него предикат P(x, y) = “город x – крупный научный центр области y”, а математик – P(x, y) = “x·y = 5”. Таким образом, возникают две различные интерпретации одной и той же формулы. В первом случае предметная область состоит из географических объектов (x – это города, y – области), а во втором случае она состоит из математических объектов (x и y – это числа). В каждом случае вместо предикатного символа используются различные конкретные предикаты, заданные на указанных предметных областях, и из одной формулы получаются интерпретации, совершенно не сопоставимые друг с другом.

Поэтому так же, как и для формул исчисления высказываний, невозможно говорить об истинности той или иной формулы исчисления предикатов: одна и та же формула может быть истинной при одной интерпретации и ложной при другой, даже если эти интерпретации имеют дело с одной и той же предметной областью. Например, формула ($ x P(x, y)) истинна при любом y, если вместо P(x, y) взять предикат P(x, y) = “x + y = 5” на R: при y = y₀ она превращается в истинное высказывание ($ x x + y₀ = 5), т.к. достаточно взять x = 5 – y₀ . Но та же формула будет принимать значение ложь, если на R рассмотреть предикат P(x, y) = “x×y = 5”: при y = 0 невозможно найти такое число x, что x×0 = 5.

Итак, при выяснении вопроса об истинностных значениях формул исчисления предикатов первостепенную роль играет понятие интерпретации. Перейдём теперь к точным определениям.

Пусть Ф – некоторое (конечное) множество формул исчисления предикатов, в записи которых участвуют пропозициональные переменные a₁ , … , a_m , объектные переменные x₁ , … , x_n , имеющие хотя бы одно свободное вхождение, предикатные символы 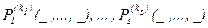от k₁ , … , k_s аргументов. Интерпретацией множества формул Фназывается упорядоченный набор

J = (M, a₁ = a₁ , … , a_m = a_m , x₁ = o₁ , … , x_n = o_n , ),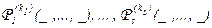

где M – некоторое фиксированное множество – предметная область интерпретации, a₁ , … , a_m – высказывания об элементах множества M (об объектах предметной области), o₁ , … , o_n – фиксированные элементы множества M (объекты этой предметной области), а 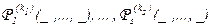– фиксированные предикаты от k₁ , … , k_s аргументов, заданные на предметной области M . Следует отметить, что одна предметная переменная может иметь, вообще говоря, несколько свободных вхождений в одной формуле, для каждого из которых в интерпретации должно быть зарезервировано своё значение.

При заданной интерпретации каждая из формул А Î Ф превращается в высказывание A_J после замены всех входящих в неё пропозициональных переменных a_i на высказывания a_i (1 £ i £ m), свободных вхождений объектных переменных x_j – на объекты o_j (1 £ j £ n), переменных, связанных кванторами, – на переменные, пробегающие множество M, связанные теми же кванторами, а всех предикатных символов 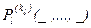– на предикаты 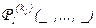(1 £ l £ s). При этом все кванторные приставки вида $ x или " x заменяются на выражения $ x Î M и " x Î M соответственно. Полученное высказывание имеет истинностное значение 0 или 1, которое называется значением истинности данной формулы при данной интерпретации .

Примеры: 1. Для одной формулы A = (" x P(x)) Ú Q(x) можно рассмотреть следующую интерпретацию: J = (M = N, x = 1, P = P( _ ), Q = Q ( _ )), где предикаты P( _ ), Q ( _ ) от одного переменного заданы на множестве N так: P(n) = “n = 2”, Q (n) = “n – нечётно”. В данном случае не нужно задавать высказывания, т.к. в формуле нет пропозициональных переменных. Для свободного вхождения объектной переменной x в этой интерпретации зарезервирован объект 1 Î N. Получаем значение формулы в данной интерпретации

A_J = (" x Î N (x = 2)) Ú (1 – нечётно) = 1.

2. Для формулы A примера 1 можно рассмотреть и другую интерпретацию, переставив предикаты P( _ ) и Q ( _ ): I = (M = N, x = 1, P = Q( _ ), Q = P( _ )). В этой интерпретации I формула имеет значение ложь:

A_I = (" x Î N (x – нечётно)) Ú (1 = 2)) = 0.

3. Рассмотрим формулу Ф = a Ù ($ x (P(x, y) « Q(x, y))) и интерпретацию:

J = (M = {0, 1}, a = “0 £ 1”, y = 1, P = P( _ , _ ), Q = Q( _ , _ )),

где “0 £ 1” – высказывание об элементах множества M, 1 – фиксированный объект множества M, а предикаты P( _ , _ ), Q( _ , _ ) от двух аргументов заданы на M следующим образом: P(u, v) = “u×v = 1”, Q(u, v) = “u = v”. В этой интерпретации значение формулы таково:

Ф_J = “0 £ 1” Ù ($ x Î {0, 1} ((x×1 = 1) « (x = 1))) = 1.

4. Ещё одна интерпретация для формулы предыдущего примера:

I = (M = {0, 1}, a = “0×0 = 1×1”, y = 0, P = P( _ , _ ), Q = Q( _ , _ ))

с теми же предикатами. В этой интерпретации формула превращается в высказывание Ф_I = “0×0 = 1×1” Ù ($ x Î M ((x×0 = 1) « (x = 0))), которое ложно, поскольку ложно высказывание “0×0 = 1×1”. Следует отметить, что высказывание $ x Î M ((x×0 = 1) « (x = 0)) истинно, т.к. при x = 1 верно (1×0 = 1) « (1 = 0) – оба аргумента эквивалентности ложны.

5.Если рассмотреть интерпретацию

K = (M = {0, 1}, a = “0×0 = 1×0”, y = 0, P = P( _ , _ ), Q = Q( _ , _ )),

то формула примера 3 имеет значение

Ф_K = “0×0 = 1×0” Ù ($ x Î M ((x×0 = 1) « (x = 0))) = 1,

т.к. оба высказывания “0×0 = 1×0” и ($ x Î M ((x×0 = 1) « (x = 0))) истинны.

6.Интерпретация формулы Ф(a₁ , … , a_n ) исчисления высказываний имеет вид J = (M, a₁ = a₁ , … , a_n = a_n ), где M – некоторое множество, а a₁ , … , a_n – высказывания об элементах этого множества, подставляемые вместо пропо­зи­циональных переменных a₁ , … , a_n . По существу она совпадает с прежней интерпретацией e = (e₁ ; … ; e_n), где e_i – значение истинности для высказывания a_i (1 £ i £ n).Таким образом, введённое более общее понятие интерпретации формул исчисления предикатов согласуется с использованным ранее понятием интерпретации формул исчисления высказываний.

Ясно, что при любой интерпретации значением Ф(a₁ , … , a_n ) тождественно истинной формулы исчисления высказываний будет 1, а значение тождественно ложной формулы будет равно 0. В то же время выполнимые формулы исчисления высказываний могут при разных интерпретациях принимать различные значения. Например, выполнимая формула (a Ù b) принимает значение 1 при интерпретации J = (M = {0, 1}, a = “0 = 0”, b = “1 = 1”), и имеет значение 0 при интерпретации I = (M = {0, 1}, a = “0 ¹ 0”, b = “1 = 1”).

Теперь можно ввести классификацию формул, аналогичную той, которая была использована для формул исчисления высказываний.

Формула исчисления предикатов называется тождественно истинной (или общезначимой), если она принимает значение 1 в любой интерпретации. Формула называется тождественно ложной (или противоречием), если она принимает значение 0 при любой интерпретации. Если формула не тождественно истинна и не тождественно ложна, то она называется выполнимой.

Две формулы исчисления предикатов называются равносильными, если они принимают одинаковые значения при любой интерпретации этой пары формул.

Примеры: 1.Любой закон логики исчисления высказываний является общезначимой формулой, а любая тождественно ложная формула исчисления высказываний – противоречием.

2. Формула " x (P(x) ® Q(x)), рассмотренная выше, выполнима, т.к. в одних интерпретациях принимает значение 1, а в других – значение 0.

3.Формула 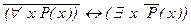общезначима. Это следует из того, что при любой интерпретации J = (M, P = P( _ )) значением этой формулы будет высказывание 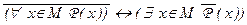, которое истинно ввиду доказанных ранее равносильностей с предикатами и кванторами.

4.Из 3 следует (?!), что .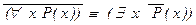

5. Основные равносильности с кванторами дают примеры равносильных формул, если исключить из них отношения принадлежности переменных множествам и вместо предикатов рассматривать предикатные символы. Например, равносильность " x Î A (P(x, y) Ù Q(x, y)) º (" x Î A P(x, y)) Ù (" x Î A Q(x, y)) даёт равносильные формулы " x (P(x, y) Ù Q(x, y)) º (" x P(x, y)) Ù (" x Q(x, y)).

Действительно, если рассмотреть любую интерпретацию

J = (M, y₁ = o₁ , … , y_n = o_n , P = P⁽ⁿ⁺¹⁾(_ , … , _ ), Q = Q⁽ⁿ⁺¹⁾(_ , … , _ )),

то " x Î M (P(x, y) Ù Q(x, y)) º (" x Î M P(x, y)) Ù (" x Î M Q(x, y)) по теореме об основных равносильностях с кванторами, а значит

(" x (P(x, y) Ù Q(x, y)))_J = ((" x P(x, y)) Ù (" x Q(x, y)))_J .

6. Для любой формулы исчисления предикатов существует равносильная ей формула, в которой каждая объектная переменная либо свободна, либо связана, т.е. любая переменная не может иметь двух вхождений, в одном из которых она свободна, а в другом – связана.

Для доказательства достаточно, пользуясь утверждением (0) из теоремы об основных равносильностях с кванторами заменить все вхождения связанных переменных в области действия связывающего их квантора на вхождения уникальных переменных (не встречающихся в других местах формулы), связанных теми же кванторами с теми же областями действия. Например,

P(x, y, z)® (($ x Q(x, z)) Ú (" z P(x, y, z))) º

º P(x, y, z) ® (($ u Q(u, z)) Ú (" v P(x, y, v))).

В последней формуле переменные x, y, z свободны, а u и v – связаны.

7. Формула Ф общезначима тогда и только тогда, когда 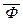тождественно ложна.

8. Формула " x ($ y P(x, y)) выполнима. В самом деле, её значение 1 при интерпретации (N, P = P( _ , _ )), где P( x , y) = “x < y”, и значение 0 – при интерпретации (N, P = Q( _ , _ )), где Q( x , y) = “x > y”. Действительно, значением при первой интерпретации будет (" x Î N ($ y Î N (x < y))) = 1 – высказывание, выражающее факт неог­ра­ниченности натурального ряда. А её значение при второй интерпретации (" x Î N ($ y Î N (x > y))) = 0, поскольку при x = 1 найти меньший элемент y Î N невозможно.

Можно ввести и понятие логического следования для формул исчисления предикатов: говорят, что формула A является логическим следствием формул A₁ , … , A_n (пишут A₁ , … , A_n A), если для любой интерпретации множества формул Ф = {A₁ , … , A_n , A}, в которой все формулы-посылки A₁ , … , A_n принимают значение истина, формула-заключение А также принимает значение истина. Если нет ни одной интерпретации, в которой все формулы A₁ , … , A_n принимают значение истина, то A считается логическим следствием формул A₁ , … , A_n по определению. Как и для формул исчисления высказываний, используется и запись вида Г A, где Г = {A₁ , … , A_n }. В случае Г = Æ запись A означает, что формула А общезначима. Легко понять, что введённые понятия согласуются с соответствующими понятиями для формул исчисления высказываний.

Теорема (критерий логического следования). A₁ , … , A_n A тогда и только тогда, когда формула (A₁ Ù … Ù A_n ® A) тождественно истинна.

Доказательство. Если A₁ , … , A_n A , то при любой интерпретации множества формул Ф = {A₁ , … , A_n , A}, в которой все формулы-посылки A₁ , … , A_n принимают значение истина, формула-заключение А также принимает значение истина. Поэтому формула (A₁ Ù … Ù A_n ® A) принимает значение истина для любой интерпретации, при которой значение истина принимает формула (A₁ Ù … Ù A_n). Если же интерпретация такова, что формула A₁ Ù … Ù A_n принимает значение ложь, то импликация (A₁ Ù … Ù A_n ® A) в этой интерпретации всё равно принимает значение истина. Таким образом, эта формула-импликация принимает значение истина при любой интерпретации, т.е. она тождественно истинна.

Обратно, если формула (A₁ Ù … Ù A_n ® A) имеет значение истина при любой интерпретации, то при интерпретации множества Ф = {A₁ , … , A_n , A}, в которой все формулы-посылки A₁ , … , A_n принимают значение истина, будет истинна и конъюнкция A₁ Ù … Ù A_n . Поэтому из истинности в этой интерпретации импликации (A₁ Ù … Ù A_n ® A) получим истинность в рассматриваемой интерпретации и формулы А, т.е. логическое следование A₁ , … , A_n A имеет место.

Теорема доказана.

Теорема (о дедукции). Для любого множества формул Г и формул А, B условие Г, А В выполнено тогда и только тогда, когда Г A ® B.

Доказательство. Если Г = Æ, то А В Û (A ® B тождественно истинна) Û A ® B.

Если Г = {A₁ , … , A_n} ¹ Æ, то Г, А В Û (A₁ Ù … Ù A_n Ù А ® B тождественно истинна) Û (A₁ Ù … Ù A_n ® (А ® B) тождественно истинна) Û Û Г A ® B. Здесь использованы равносильности

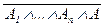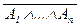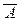(A₁ Ù …Ù A_n Ù A ® B) º Ú B º Ú Ú B º

º 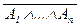Ú (A ® B) º A₁ Ù …Ù A_n ® (A ® B).

Теорема доказана.

Примеры: 1. (" x A(x)) A(y), где переменная y не совпадает с x.

Рассмотрим произвольную интерпретацию формулы ((" x A(x)) ® A(y)):

J = (M, a₁ = a₁ , … , a_m = a_m , x₁ = o₁ , … , x_n = o_n , ),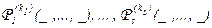

Если значение формулы (" x A(x)) в этой интерпретации ложно: (" x A(x))_J = 0, то значение формулы-импликации истинно. Если же (" x A(x))_J = 1, то для любого объекта u Î M верно A(u)_J = 1, в частности, это верно и для u = o, т.е. A(y)_J = A(o)_J = 1. Поэтому рассматриваемая формула-импликация принимает в интерпре­тации J значение истина, т.е. является тождественно истинной. Значит, логическое следование (" x A(x)) A(y) имеет место.

2. Докажите, что A(y) ($ x A(x)), где переменная y не совпадает с x.

3. (A(x) ® B) (($ x A(x)) ® B), где формула B не зависит от x.

Рассмотрим любую интерпретацию

J = (M, a₁ = a₁ , … , a_m = a_m , x₁ = o₁ , … , x_n = o_n , ),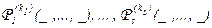

формулы (A(x) ® B) ® (($ x A(x)) ® B). Если значение формулы A(x) ® B в этой интерпретации ложно, то значение рассматриваемой формулы-импликации истинно. Если же (A(x) ® B)_J = 1, то истинно и значение импликации (($ x A(x)) ® B), т.к. можно взять x = o, а значит, истинно и значение всей рассматриваемой формулы-импликации (A(x) ® B) ® (($ x A(x)) ® B). Поэтому логическое следование (A(x) ® B) (($ x A(x)) ® B) имеет место.

4. Условие на формулу B в примере 3 существенно. Например, если B = A(x), то формула A(x) ® B тождественно истинна, но импликация ($ x A(x)) ® A(x) принимает значение истина не всегда: например, если J = (M = Z, x = –1, A = (x > 0)), тоэта формула превращается в ложное высказывание ($ x Î Z (x > 0)) ® (–1 > 0).

5. Докажите, что (B ® A(x)) (B ® (" x A(x))), где B не зависит от x.

Точно так же, как для исчисления высказываний, можно рассматривать правила логического вывода для исчисления предикатов.

Например, предыдущие примеры доказывают следующие правила логического вывода с предикатами:

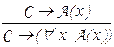(введение квантора " ), 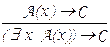(введение квантора $ ), где С не содержит вхождений переменной x.

Упражнение:Придумайте несколько других правил логического вывода с кванторами в исчислении предикатов.