Теорема (об основных равносильностях с кванторами).

(0) " x Î A P(x, y) º " z Î A P(z, y), $ x Î A P(x, y) º $ z Î A P(z, y), где P(x, y) не зависит от z,

(1) " x Î A (" y Î A P(x, y, z)) º " y Î A (" x Î A P(x, y, z)),

$ x Î A ($ y Î A P(x, y, z)) º $ y Î A ($ x Î A P(x, y, z))

(для разноимённых кванторов утверждения не верны),

(2) 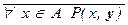º $ x Î A 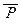(x, y), $ x Î A P(x, y) º ,

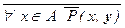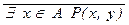º " x Î A 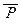(x, y), " x Î A P(x, y) º ,

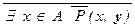(3) (" x Î A P(x, y)) Ù (" x Î A Q(x, y)) º " x Î A (P(x, y) Ù Q(x, y))

(для связкиÚ утверждение не верно),

(4) ($ x Î A P(x, y)) Ú ($ x Î A Q(x, y)) º $ x Î A (P(x, y) Ú Q(x, y))

(для связкиÙ утверждение не верно),

(5) (" x Î А Р(х, y)) Ú R(y) º " x Î A (P(x, y) Ú R(y)),

($ x Î А Р(х, y)) Ú R(y) º $ x Î A (P(x, y) Ú R(y)),

(6) (" x Î А Р(х, y)) Ù R(y) º (" x Î А (Р(x, y) Ù R(y)),

($ x Î А Р(х, y)) Ù R(y) º ($ x Î А (Р(x, y) Ù R(y)),

(7) " х Î А (R(y)® Р(х, y)) º R(y)® (" x Î А Р(х, y)),

$ х Î А (R(y) ® Р(х, y)) º R(y) ® ($ x Î А Р(х, y))

(8) (" x Î А Р(х, y)) ® R(y) º ($ x Î А (Р(x, y) ® R(y)),

($ x Î А Р(х, y)) ® R(y) º (" x Î А (Р(x, y) ® R(y))

(всюду жирные буквы обозначают, вообще говоря, наборы переменных, которые могут и отсутствовать, в равносильностях (5)–(8) предикат R(y) не зависит от x).

Доказательство. Все равносильности доказываются единообразно, исходя из определений истинностных значений предикатов с кванторами и равносильности предикатов.

(0) Области истинности обоих предикатов $ x Î A P(x, y) и $ z Î A P(z, y) состоят из тех наборов а = (a₁ ; … ; a_n) Î Aⁿ, при которых найдётся элемент b Î A со свойством P(b, a) = 1, а значит, эти области истинности совпадают.

(1) Область истинности предиката " x Î A (" y Î A P(x, y, z)) состоит из всех наборов а = (a₁ ; … ; a_n) Î Aⁿ , при которых предикат " y Î A P(c, y, a) имеет значение 1 при любом с Î A, т.е. из всех наборов а Î Aⁿ со свойством P(c, d, a) = 1 при любых c, d Î A.

Точно так же область истинности предиката " y Î A (" x Î A P(x, y, z)) состоит из всех наборов а = (a₁ ; … ; a_n) Î Aⁿ , при которых предикат " x Î A P(x, d, a) принимает значение 1 при любом d Î A, т.е. из тех наборов а Î Aⁿ, при которых P(c, d, a) = 1 при любых c, d Î A.

Сравнение выводов, сделанных в предыдущих абзацах, доказывает (1).

(2) Область истинности предиката 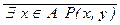состоит из всех таких наборов а = (a₁ ; … ; a_n) Î Aⁿ , для которых предикат $ x Î A P(x, a) принимает значение 0, т.е. из всех таких наборов а Î Aⁿ, при которых P(c, a) = 0 при любом c Î A. Но множество всех таких наборов образует и множество истинности предиката " x Î A 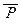(x, y), что и доказывает равносильность рассматриваемых предикатов.

(3) Область истинности предиката (" x Î A P(x, y)) Ù (" x Î A Q(x, y)) состоит из всех наборов а = (a₁ ; … ; a_n) Î Aⁿ, при которых (" x Î A P(x, a)) = 1 = = (" x Î A Q(x, a)), т.е. из всех a Î Aⁿ, для которых P(c, a) = 1 = Q(c, a) при любом c Î A. Это множество наборов совпадает с множеством истинности исследуемого предиката " x Î A (P(x, y) Ù Q(x, y)).

(5) Область истинности предиката (" x Î А Р(х, y)) Ú R(y) состоит из множества всех таких а = (a₁ ; … ; a_n) Î Aⁿ , для которых либо R(a) = 1, либо P(c, a) = 1 при любом с Î A. По определению дизъюнкции, это значит, что (P(c, a) Ú R(a)) = 1 при любом c Î A, т.е. множество рассматриваемых наборов a Î Aⁿ совпадает с областью истинности предиката " x Î A (P(x, y) Ú R(y)).

(6) Область истинности предиката ($ x Î А Р(х, y)) Ù R(y) состоит из множества всех таких а = (a₁ ; … ; a_n) Î Aⁿ , для которых P(c, a) = 1 при некотором с Î A и R(a) = 1. Это значит, что (Р(с, a) Ù R(a)) = 1, т.е. мнжество рассматриваемых наборов a Î Aⁿ совпадает с областью истинности предиката $ x Î А (Р(x, y) Ù R(y)).

(7) (" х Î А (R(y) ® Р(х, y))) º (" x Î A ( 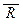(y)Ú P(x, y))) º

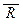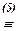º (" x Î A (P(x, y) Ú (y))) ((" x Î А Р(х, y)) Ú 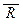(y)) º

º ( 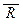(y) Ú (" x Î А Р(х, y))) º (R(y) ® (" x Î А Р(х, y))).

(8) (($ x Î А Р(х, y)) ® R(y)) º ((" x Î A 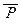(x, y)) Ú R(y))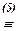

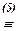(" x Î A ( 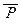(x, y) Ú R(y))) º (" x Î А (Р(x, y) ® R(y))).

Теорема доказана.

Замечание:Утверждения пункта (0) доказанной теоремы носят общематематический характер: не важно как обозначать связанную переменную. Так, результат суммирования не зависит от обозначения индекса суммирования, а интеграл – от переменной интегрирования.

Приведём примеры, показывающие существенность ограничений в доказанной теореме:

Примеры: 1. " x Î R ($ y Î R x > y) 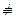$ y Î R (" x Î R x > y), т.к. левая часть истинна, а правая – ложна.

2. (" x Î R x > 0) Ú (" x Î R x £ 0) 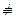" x Î R (x > 0) Ú (x £ 0), т.к. левая часть ложна, а правая – истинна.

3. ($ x Î R x > 0) Ù ($ x Î R x £ 0) 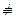$ x Î R (x > 0) Ù (x £ 0), т.к. левая часть истинна, а правая – ложна.

4.Следующие равносильности не верны:

" х Î А (Р(х) ® R) 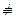(" x Î А Р(х)) ® R,

$ х Î А (Р(х) ® R) 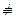($ x Î А Р(х)) ® R,

" х Î А (Р(х) « R) 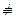(" x Î А Р(х)) « R,

$ х Î А (Р(х) « R) 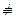($ x Î А Р(х)) « R.

Действительно, пусть R º 0, P(x) = “x = 0”, A = R. Тогда P(x) ® R º “x ¹ 0”, и

" х Î А (Р(х) ® R) º " x Î R (x ¹ 0) – ложно, а (" x Î А Р(х)) ® R º º 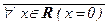º $ x Î R x ¹ 0 –истинно.

$ х Î А (Р(х)® R) º $ х Î R (х ¹ 0) – истинно, а ($ x Î А Р(х))® R º º 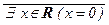º " x Î R x ¹ 0 – ложно.

" х Î А (Р(х) « R) º " х Î R (x ¹ 0) – ложно, а (" x Î А Р(х)) « R º º 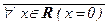º $ x Î R x ¹ 0 – истинно.

$ х Î А (Р(х) « R) º $ х Î R (х ¹ 0) – истинно, а ($ x Î А Р(х)) « R º º 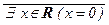º " x Î R x ¹ 0 – ложно.

Таким образом, при преобразовании формул нужно осторожно обращаться с кванторами там, где стоят логические связки импликации и эквивалентности.

5. Если предикат R зависит от x, то равносильности (5)–(8) могут быть не верны. Например,

(" x Î R (х < y)) Ú (x = y) º (x = y) 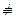0 º " x Î R ((x < y) Ú (x = y)),

($ x Î N (х < 1)) Ú (x = 1) º (x = 1) 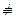1º $ x Î N ((x < 1) Ú (x = 1)).

Примеры существенности условий теоремы для равносильностей (6)–(8) приведите самостоятельно.