Язык исчисления предикатов

С помощью предикатов можно формулировать содержательные утверждения в различных областях знания. Поэтому важно дать средства построения осмысленных выражений с предикатами и приписывания им истинностных значений подобно тому, как это было сделано в исчислении высказываний.

Здесь возникает одна проблема: поскольку предикаты в разных областях знания совершенно разные, то при построении исчисления предикатов нужно отвлечься от специфики конкретных предикатов, рассматривая запись P(x₁ , … , x_n ) как абстрактный символ предиката P от n переменных x₁ , … , x_n , вместо которого в каждой науке можно подставлять те или иные её специфические предикаты от n переменных. Например, предикатный символ P(x, y) географ может наполнить своим содержанием, рассматривая конкретный предикат P(x, y) = “река х впадает в море y”, а математик – своим, полагая P(x, y) = “x > y”.

Алфавит языка исчисления предикатовсодержит несколько групп символов:

I. Пропозициональные переменные: a, b, c₉₉ , d₃₄₅ , … для обозначения высказываний.

II. Объектные переменные: x, y, z₉₉ , t₃₄₅ , … для обозначения объектов предметной области той или иной науки.

III. Логические связки: 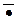– отрицание, Ù – конъюнкция, Ú – дизъюнкция, ® – импликация и « – эквивалентность.

IV. Предикатные символы: P⁽¹⁾( _ ), Q⁽¹⁾( _ ), R⁽¹⁾( _ ), … , P⁽²⁾( _ , _ ), Q⁽²⁾( _ , _ ), R⁽²⁾( _ , _ ), … для обозначения предикатов от любого числа переменных (количество переменных, если это необходимо, указано в скобках в верхнем индексе).

V. Кванторы: " – квантор всеобщности и $ – квантор существования.

VI. Служебные символы: ( , ) – скобки и запятая , .

Как и в языке исчисления высказываний, осмысленными фразами в языке исчисления предикатов будут формулы. Понятие формулы языка исчисления предикатовстроится от простого к сложному с помощью следующих правил, в которых одновременно даётся определение свободных и связанных вхождений объектных переменных. Термин вхождение объектной переменной обозначает любое место в последовательности символов формулы, где встречается данная переменная:

(Ф1): любая формула исчисления высказываний (от пропозициональных переменных) является формулой исчисления предикатов, в которой нет объектных переменных и кванторов.

(Ф2): если P⁽ⁿ⁾( _ , … , _ ) – предикатный символ от n переменных и x₁ , … , x_n – объектные переменные, то P⁽ⁿ⁾( x₁ , … , x_n ) – формула исчисления предикатов, в которой все вхождения объектных переменных x₁ , … , x_n свободны, а вхождений других объектных переменных нет.

(Ф3): если A и В – две формулы, то (A Ù B), (A Ú B), (A ® B), (A « B), 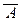, 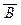– тоже формулы, в которых свободны все вхождения объектных переменных, свободные в А или в В, и связаны все вхождения объектных переменных, связанные в А или в В.

(Ф4): если A(x) – формула хотя бы с одним свободным вхождением объектной переменнойx, то выражения (" x A(x)) и ($ x A(x)) – формулы, в которых связаны вхождения всех объектных переменных, связанных в А, а также все вхождения x, и свободны все вхождения объектных переменных, свободные в А, кроме переменной х. При этом формула A(x) называется областью действия квантора.

(Ф5): других формул нет.

Будем называть объектную переменную в формуле свободной (связанной), если свободны (связаны) все её вхождения в этой формуле.

Примеры: 1.Если a – пропозициональная переменная, то ($ x (P(x) « a)) – формула исчисления предикатов, образованная по правилу (Ф4) из формулы (P(x) « a) со свободным вхождением объектной переменной x. В полученной формуле ($ x (P(x) « a)) нет свободных вхождений объектных переменных.

2. " x P(x) ® ($ y Q(y)) – не формула, т.к. в ней не хватает скобок.

3. ($ y (P(x) Ú (" y (Q(x) ® R(y))))) – не формула: в ней квантор $ навешивается на переменную y, у которой нет свободных вхождений.

4. (" x ((" y Q(y)) « ($ x (Q(y) Ù R(x))))) – не формула (?!), но (" y ((" y Q(y)) « ($ x (Q(y) Ù R(x))))) – формула, в которой нет свободных вхождений объектных переменных. Такие формулы называются замкнутыми.

5.((" x P(x, y)) Ú Q(x, z)) – формула, в которой свободно вхождение объектной переменной y, вхождение переменной x в формулу (" x P(x, y)) связано, а вхождение переменной x в формулу Q(x, z) свободно, как и вхождение z.

6. (" x ((" y Q(y, v)) « ($ z (Q(z, u) Ù R(x, t))))) – формула со свободными переменными v, u, t.

7. ($ x (" y (Q(y, v)« (" z Q(z, x))))) – формула со свободной переменной v.

В формулах примеров 1и 4 нет свободных переменных, в формуле примера 5 свободна объектная переменная z, в формуле примера 6 – переменные v, u, t, а в формуле примера 6 – переменная v.

Как и ранее, будем опускать внешние скобки в записи формул, остальные скобки в сложных формулах рекомендуется сохранять.