Равносильные и тождественно истинные предикаты

Два предиката P(x₁ , … , x_n ) и Q(x₁ , … , x_n ), определённые на множестве А (т.е. предикаты с условиями Aⁿ Í D(P) Ç D(Q)),называют равносильными на множествеА и пишут при этом P(x₁ , … , x_n ) º_А Q(x₁ , … , x_n ), если выполнено равенство D₁(P) Ç Aⁿ = D₁(Q) Ç Aⁿ , другими словами, если " a₁ , … , a_n Î A (P(a₁ , … , a_n ) = 1 « Q(a₁ , … , a_n ) = 1). Если D(P) = Aⁿ = D(Q), товместо P(x₁ , … , x_n ) º_А Q(x₁ , … , x_n ) будем кратко писать P(x₁ , … , x_n ) º Q(x₁ , … , x_n ).

Если Aⁿ Í D₁(P), т.е. " a₁ , … , a_n Î A P(a₁ , … , a_n ) = 1, то предикат P(x₁ , … , x_n ) называется тождественно истинным на множествеA : P(x₁ , … , x_n ) º_А 1. Аналогично, предикат P(x₁ , … , x_n ) называют тождественно ложным на множествеA: P(x₁ , … , x_n ) º_А 0, если Aⁿ Í D₀(P), т.е. выполнено условие " a₁ , … , a_n Î A P(a₁ , … , a_n ) = 0 .

Примеры: 1.Равносильны ли предикаты P(x) = “ > 1” и Q(x) = “x < 1” на множестве R₊ = {r Î R | r > 0} = (0; +∞) ?

Во-первых, оба предиката определены на R₊ : D(P) = R \ {0}, D(Q) = R . Найдём их области истинности. Для предиката Q ясно, что D₁(Q) = (–∞; 1). Для предиката P имеем: 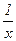> 1 Û 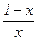> 0 Û x×(1–x) > 0 Û x Î (0; 1). Хотя получили, что D₁(P) ¹ D₁(Q), но

D₁(P) Ç R₊ = (0; 1) Ç (0; +∞) = (0; 1) = (–∞; 1) Ç (0; +∞) = D₁(Q) Ç R₊,

так что P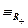(x) Q(x).

2. Рассмотренные выше предикаты P(x) и Q(x) не равносильны намножестве A = R \ {0}: D₁(P) Ç A = (0; 1) ¹ (–∞; 1) \ {0} = D₁(Q) Ç A .

3.Предикат Q(x) тождественно истинен на R_– = {r Î R | r < 0} = (–∞; 0).

Действительно, R_– Í D₁(Q) = (–∞; 1).

4. Предикат P(x) тождественно ложен на множестве (1; +∞).

5. Предикаты P(x, y) = “x×y Î Z” и Q(x, y) = “x Î Z Ù y Î Z” равносильны на множестве A = Z, но не равносильны на множестве R.

В самом деле, оба предиката определены на R, точнее D(P) = R´R = D(Q), и тождественно истинны на Z : высказывания " a, b Î Z a×b Î Z и " a, b Î Z (a Î Z) Ù (b Î Z)обаистинны. Поэтому P(x) º_Z Q(x). С другой стороны, D₁(Q) = Z´Z ¹ D₁(P): например, (0,5; 2) Î D₁(P) \ Z´Z .

Упражнения: 1. Докажите, что P(x) º_А Q(x), где A = (0; 10), P(x) = “x > 0,5”, Q(x) = “x² > 0,5×x”.

2. Равносильны ли на R₊ , Rпредикаты из предыдущего упражнения ?

3. Верно ли, что P(x₁ , … , x_n ) º_А Q(x₁ , … , x_n ) тогда и только тогда, когда (P ® Q) º_A 1 ? А если (P « Q) º_A 1 ?

4. Равносильны ли предикаты P(x, y) = “x×y = 1” и Q(x, y) = “x = 1 / y” на множествах R, R \ {0}, N?

Приведём некоторые основные равносильности предикатов с кванторами.