Логические операции над предикатами
Если заданы два предиката P(x1 , … , xn ) и Q(x1 , … , xn) с одной и той же областью определения An и одним и тем же набором переменных, то можно рассмотреть предикаты 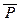 (x1 , … , xn), (P Ù Q)(x1 , … , xn), (P Ú Q)(x1 , … , xn), (P ® Q)(x1 , … , xn), (P « Q)(x1 , … , xn), называемые соответственно отрицанием предикатаP, а также конъюнкцией, дизъюнкцией, импликацией и эквивалентностью предикатовP и Q. Эти новые предикаты определяются следующим образом: для любых a1 , … , an Î A полжим
(x1 , … , xn), (P Ù Q)(x1 , … , xn), (P Ú Q)(x1 , … , xn), (P ® Q)(x1 , … , xn), (P « Q)(x1 , … , xn), называемые соответственно отрицанием предикатаP, а также конъюнкцией, дизъюнкцией, импликацией и эквивалентностью предикатовP и Q. Эти новые предикаты определяются следующим образом: для любых a1 , … , an Î A полжим 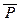 (a1 , … , an) =
(a1 , … , an) = 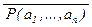 и при w Î {Ù , Ú , ® , « } (P w Q)(a1 , … , an) = (P(a1 , … , an) w Q(a1 , … , an)).
и при w Î {Ù , Ú , ® , « } (P w Q)(a1 , … , an) = (P(a1 , … , an) w Q(a1 , … , an)).
Примеры: 1. Пусть на Rзаданы два предиката: P(x) = “x > 3” и Q(x) = = “x £ 5”. Тогда для любого a Î Rимеем
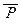 (a) =
(a) = 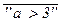 = “a £ 3”,
= “a £ 3”, 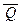 (a) =
(a) = 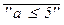 = “a > 5”,
= “a > 5”,
(PÙQ)(a) = “a > 3” Ù “a £ 5” = “3 < a £ 5”,
(PÚQ)(a) = “a > 3” Ú “a £ 5” = “a Î R” = 1,
(P®Q)(a) = “a > 3” ® “a £ 5” º 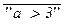 Ú “a £ 5” = “a £ 3” Ú “a £ 5” = “a £ 5”,
Ú “a £ 5” = “a £ 3” Ú “a £ 5” = “a £ 5”,
(P«Q)(a) = “a > 3”« “a £ 5” º ( 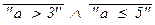 ) Ú (“a > 3” Ù “a £ 5”) =
) Ú (“a > 3” Ù “a £ 5”) =
= (“a £ 3”Ù“a > 5”) Ú “3 < a £ 5” º 0 Ú “3 < a £ 5” º “3 < a £ 5”.
Ясно, что в этом примере верны следующие равенства множеств:
D1( 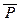 ) = D0(P), D0(
) = D0(P), D0( 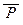 ) = D1(P), D1(PÙQ) = D1(P) Ç D1(Q),
) = D1(P), D1(PÙQ) = D1(P) Ç D1(Q),
D0(PÙQ) = D0(P) È D0(Q), D1(PÚQ) = D1(P) È D1(Q), D1(P®Q) = D0(P) È D1(Q),
D1(P«Q) = (D1(P) Ç D1(Q)) È (D0(P) Ç D0(Q)) (проверьте !!).
2. Пусть P(x, y) = “x2 < y”, Q(x, y) = “y £ x” – два предиката на Z. Вычислим предикат P ® Q и его область истинности.
По определению для любых a, b Î Z :(P ® Q)(a, b) = (P(a, b) ® Q(a, b)) = = “a2 < b” ® “b £ a” º 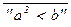 Ú “b £ a” º “a2 ³ b” Ú “b £ a”. Когда истинна последняя дизъюнкция ? Она истинна, если b £ a. Но учитывая, что a Î Z, имеем a £ a2, так что из b £ a следует b £ a2, и (P ® Q)(a, b) º “b £ a ”.
Ú “b £ a” º “a2 ³ b” Ú “b £ a”. Когда истинна последняя дизъюнкция ? Она истинна, если b £ a. Но учитывая, что a Î Z, имеем a £ a2, так что из b £ a следует b £ a2, и (P ® Q)(a, b) º “b £ a ”.
Как и ранее, нетрудно понять, что D1(P ® Q) = D0(P) È D1(Q).
Оказывается, что отмеченные в этих примерах соотношения, связывающие множества D1(P w Q) и D1(P), D1(Q), D0(P), D0(Q), справедливы всегда.
Лемма (об областях истинности).Пусть P(x1 , … , xn), Q(x1 , … , xn) – два предиката на множестве А. Тогда верны равенства множеств:
D1( 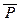 ) = D0(P) = D(P) \ D1(P),
) = D0(P) = D(P) \ D1(P),
D1(P Ù Q) = D1(P) Ç D1(Q),
D1(P Ú Q) = D1(P) È D1(Q),
D1(P ® Q) = D0(P) È D1(Q),
D1(P « Q) = (D1(P) Ç D1(Q)) È (D0(P) Ç D0(Q)).
Доказательство. Все равенства доказываются однообразно, исходя из определения области истинности и логических операций над предикатами. Например,
D1( 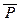 ) = {(a1 ; … ; an) Î An |
) = {(a1 ; … ; an) Î An | 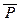 (a1 , … , an) = 1} =
(a1 , … , an) = 1} =
= {(a1 ; … ; an) Î An | P(a1 , … , an) = 0} = D0(P) = D(P) \ D1(P) = An \ D1(P),
что и требовалось.
Аналогично доказываются и остальные равенства множеств (в приводимых ниже вычислениях для краткости полагаем a = (a1 ; … ; an), P(a) = P(a1 ; … ; an)):
D1(P Ù Q) = {(a1 ; … ; an) Î An | (PÙQ)(a1 , … , an) = 1} =
= { aÎ An | (P(a) Ù Q(a)) = 1} = { aÎ An | (P(a) = 1) Ù (Q(a) = 1)} =
= { a Î An | P(a) = 1} Ç { a Î An | Q(a) = 1} = D1(P) Ç D1(Q),
D1(P « Q) = { a Î An | (P « Q)(a) = 1} = { a Î An | (P(a) « Q(a)) = 1} =
= {a Î An | ((P(a) Ù Q(a)) Ú ( 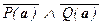 )) = 1)} =
)) = 1)} =
= {a Î An | (P(a) Ù Q(a) = 1) Ú ( 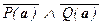 = 1)} =
= 1)} =
= {a Î An | P(a) Ù Q(a) = 1} È {a Î An | 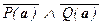 = 1} =
= 1} =
= ({a Î An | P(a) = 1} Ç {a Î An | Q(a) = 1}) È
È ({a Î An | 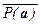 = 1} Ç {a Î An |
= 1} Ç {a Î An |  = 1}) =
= 1}) =
= (D1(P) Ç D1(Q)) È ({a Î An | P(a) = 0} Ç {a Î An | Q(a) = 0}
= (D1(P) Ç D1(Q)) È (D0(P) Ç D0(Q)).
Лемма доказана.
Упражнения: 1.Вычислите области истинности предикатов P, Q , 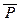 ,
, 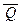 , P Ù Q , P Ú Q , P ® Q , P « Q , где P(x) = “x2 > x ”, Q(x) = “x2 – 4×x + 3 < 0”.
, P Ù Q , P Ú Q , P ® Q , P « Q , где P(x) = “x2 > x ”, Q(x) = “x2 – 4×x + 3 < 0”.
2. Прочувствуйте аналогию между логическими операциями над предикатами и операциями над множествами. Сформулируйте общее правило вычисления области истинности предиката, полученного с помощью логических связок из известных предикатов.
3.Сформулируйте и докажите лемму об областях ложности.
Рассмотренные логические операции над предикатами позволяют по заданным на множестве А предикатам строить новые предикаты. Другой способ построения новых предикатов дают кванторы. Квантор существования$ и квантор всеобщности" – это специальные математические знаки, служащие для сокращённого обозначения выражений “существует” и “для любого” соответственно.
Примеры: 1. Фразу “квадрат любого действительного числа неотрицателен” математики записывают так: " x Î R x2 ³ 0 (читается: для любого действительного числа x выполнено свойство x2 ³ 0).
2.Запись " m Î Z ($ n Î Z n < m) (читается: для любого целого числа m существует целое число n со свойством n < m)выражает тот факт, что у любого целого числа есть предшествующие ему целые числа.
В приведённых примерах написанные с помощью кванторов формулы являлись высказываниями. Оба этих высказывания были истинны, но не следует думать, что все высказывания, записанные с помощью кванторов истинны: почувствуйте разницу, прочитав и осмыслив следующие высказывания " x Î Z x ³ 0, " m Î N ($ n Î N n < m), " x Î R ($y Î R |x – y| < x).
Пусть теперь P(x) – предикат от одной переменной на множестве А. Тогда записи " x Î A P(x) (для любого x Î А выполнено свойство P(x))и $ x Î A P(x) (существует x Î А со свойством P(x)) являются высказываниями, не зависящими от переменной x. Говорят, что эти высказывания получены связыванием переменнойx с помощью квантора всеобщности " (и квантора существования $) соответственно. При этом высказывание " x Î A P(x) истинно тогда и только тогда, когда любой объектa из множества А принадлежит области истинности предиката P(x), оно ложно тогда и только тогда, когда хотя бы один объект a из множества А принадлежит области ложности предиката P(x). Высказывание $ x Î A P(x) истинно тогда и только тогда, когда хотя бы один объектa из множества А принадлежит области истинности предиката P(x), оно ложно тогда и только тогда, когда все объекты a из множества А принадлежат области ложности предиката P(x).
Примеры: 1. Если P(x) = “x делится нацело на 15” – предикат на Z, то высказывания " x Î Z P(x) и $ x Î Z P(x) ложно и истинно соответственно.
2. Если P(x) = “x2 + 6×x + 100 > 0” – предикат на R, то " x Î R P(x) – истинное высказывание. А каковы высказывания $ x Î R P(x) , " x Î R 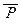 (x) ?
(x) ?
Аналогично предыдущему случаю предикатов от одной переменной можно связывать кванторами и любую переменную в предикате от n переменных, получая при этом предикат от (n–1)-й переменной: если P(x1 , … , xn ) – предикат от n переменных на множестве А, то можно, связывая переменную xi кванторами, образовать предикаты " xi Î A P(x1 , … , xn ) и $ xi Î A P(x1 , … , xn ) от (n–1)-й переменных x1 , … xi–1 , xi+1 , … , xn . Их области истинности состоят, по определению, из всех наборов (a1 ; … ; ai–1 ; ai+1 ; … ; an) Î An–1 значений переменных x1 , … xi–1 , xi+1 , … , xn , для которых при любом (соответственно хотя бы при одном) xi = a Î A истинноP(a1 , … , ai–1 ; a ; ai+1 ; … ; an ) = 1.
Примеры: 1.Если P(x, y) = “x2+y2 = 1” – предикат от двух переменных на множестве R, то предикат S(x) = (" y Î R P(x, y)) от одной переменной x принимает значение 0 (ложь) при любом x Î R(т.к., например, при y = 2 равенство x2 + y2 = 1 не верно, какой бы x Î R ни взять). Предикат T(x) = ($ y Î R P(x, y)) имеет область истинности D1(T) = [–1; 1] (при любом x = a Î [–1; 1] можно найти y = 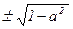 со свойством x2 + y2 = 1).
со свойством x2 + y2 = 1).
2. Пусть А – множество всех прямых на плоскости, P(x, y, z) =”прямые x, y, z имеют общую точку” – предикат от трёх переменных x, y, z на А. Тогда предикат S(x, z) = (" yÎ A P(x, y, z)) от двух переменных x, z имеет пустую область истинности (?!), а предикат T(x, z) = ($ yÎ A P(x, y, z)) обладает тем свойством, что (T(x, z) = 1)Û (x Ç z ¹ Æ).
Для удобства дальнейших рассмотрений введём следующие сокращения:
1) вместо выражения " x1 Î A (" x2 Î A ( … (" xn Î A P(x1 , … , xn))…)) будем писать " x1 , … , xn Î A P(x1 , … , xn), а $ x1 , … , xn Î A P(x1 , … , xn) – вместо $ x1 Î A ($ x2 Î A ( … ($ xn Î A P(x1 , … , xn))…)). Здесь важно, что кванторы при всех элементах x1 , … , xn однотипны, т.е. либо все являются кванторами существования, либо же все – кванторами всеобщности, а также то, что все элементы x1 , … , xn выбираются из одного и того же множества А.
2) обозначение $ ! xi Î A P(x1 , … , xi , … , xn) будет использоваться для сокращения выражения “существует единственный элемент xi во множестве А со свойством P(x1 , … , xi , … , xn)”. Формально это высказывание записывается так: ($ xi Î A P(x1 , … , xi , … , xn)) Ù (" yi Î A (P(x1 , … , yi , … , xn) ® (yi = xi ))).
Дата добавления: 2021-12-14; просмотров: 538;











