Предикаты и кванторы
Предикатном называется n – местная функция P (x1,…,xn), которая при подстановки вместо символов переменных конкретных значений из некоторого множества M превращается в высказывание, т.е. принимает значение “истина” или “ложь”. Множество М, из которого применяют значения предикатные переменные x1,…,xn, называется предметной областью предиката.
Пусть, например, P(X) обозначает одноместных предикат “x –простое число ”, предметная область M = {2,3,4…}. Тогда P(2) = “истина”, P(3) = “истина”, P(4) = “ложь”.
Пусть P(x,y) - двухместный предикат “x 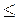 y”. Тогда P (3,5) = “истина”, P(5,3) = “ложь”.
y”. Тогда P (3,5) = “истина”, P(5,3) = “ложь”.
Множество тех наборов значений аргументов, на которых предикат принимает значение “истина”, называется областью истинности этого предиката. Область истинности двухместного предиката является бинарным отношением.
Квантор общности. Пусть P (x) – некоторые предикат, принимающий значение “истина”, или “ложь”, для каждого элемента x множества M. Тогда под выражением ("x) P(x) будем подразумевать высказывание истинное, когда P(x) истинно для каждого элемента х из множества М, и ложное – в противном случае. Читается это выражение так: “для всех х P(x)”. Это высказывание уже не зависит от х. Символ "x называется квантором общности.
Квантор существования. Пусть P(x)-некоторый предикат. Под выражением ( 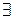 х) Р(х) будем понимать высказывание истинное, когда существует элемент множества М, для которого P(x) истинно, и ложное в противном случае. Читается это выражение так: «Существует х такое, что Р(х)» или существует х, для которого Р(х). Символ $х называется квантором существования.
х) Р(х) будем понимать высказывание истинное, когда существует элемент множества М, для которого P(x) истинно, и ложное в противном случае. Читается это выражение так: «Существует х такое, что Р(х)» или существует х, для которого Р(х). Символ $х называется квантором существования.
Покажем как определяющие алгебраическую группу условия ассоциативности, существования единичного и обратного элементов запишутся на языке кванторов:
("x) ("y) ("z) (xy)z=x(yz)
($e) ("x) ex=xe=x
("x) ($x-1) x-1 x=xx-1=e
Контрольные вопросы.
1. Дайте определение высказывание.
2. Перечислите наиболее известные тавтологии.
3. Перечислите основные методы доказательств. В чем суть каждого метода?
4. Что такое предикат?
5. Какие кванторы вы знаете?
Тест IV.
1. Высказыванием называется утверждение, имеющее значение: а)истина; б)ложь; в)истина или ложь.
2. Каким значком обозначают импликацию: а) 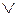 ; б)
; б) 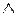 ; в)
; в) 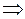 (
( 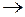 ).
).
3. Для логического значка “~” принято следующие чтение: а)”…или...“; б):”...если..., то...,”; в) “тогда и только тогда, когда...”.
4. Квантор 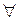 читается: а) для всех; б)существует; в)найдется.
читается: а) для всех; б)существует; в)найдется.
5.Высказывание: “существует вещественное число x, удовлетворяющее уравнению х2+1=0” в символической форме записывается:
а) 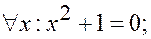 б)
б) 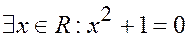 ;
;
в) 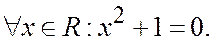
Дата добавления: 2022-02-05; просмотров: 775;











