Определение тождественности логических функций

Пример 7.Получить путем тождественных преобразований минимальную форму записи логической функции F1 и проверить, является ли она тождественной функции F2 (слайд 26).

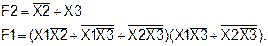
Упростим функцию F1. Так как функция F1 задана аналитически, то будем производить упрощение по шагам:

1-й шаг

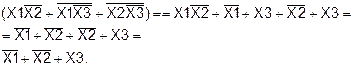
2-й шаг

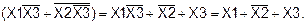
3-й шаг

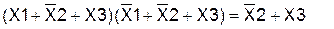
(по правилу склеивания для КНФ).

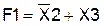(полученный результат).

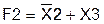(исходная функция).

Таким образом, функция F1 тождественно равна функции F2, так как совпадают их минимальные формы.

Пример 8.Получить путем тождественных преобразований логической функции F1 ее минимальную форму записи и проверить, является ли она тождественной функции F2, определенной на данных наборах (слайд 27).

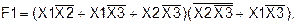
F2=1 на наборах (100), (101), (110).

1)Функция F2 определена таблично, запишем ее в СДНФ:

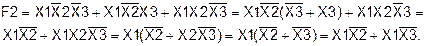
2) Упрощаем вторую скобку функции F1:

¾¾ __ __ __ __

X2X3+X1X3 = X2+X3+X1Х3 = Х2+Х3+Х1

Тогда

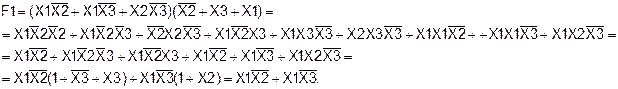
Таким образом, логическая функция F1, заданная аналитически, тождественна функции F2, заданной таблично.

Пример 9.Получить путем тождественных преобразований логической функции F2 ее минимальную форму записи и проверить, является ли она тождественной функции F1, определенной на данных наборах (слайды 28-29).

F1=0 на наборах: (000), (010), (011), (100), (110), (111)

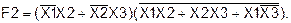
Так как F1=0 на 6 заданных наборах, то F1=1 на остальных наборах (001) и (101) (см. таблицу истинности F1):

Следовательно, нужно представить F1вСДНФ

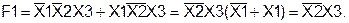
Преобразуем F2:

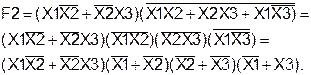
Используя основные соотношения алгебры логики (АÙА=А), можно представить функцию F2 в виде:

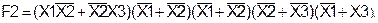
Применяя вторую форму распределительного закона ко 2-ой и 4-ой скобкам и к 3-ей и 5-ой скобкам, получим следующее:

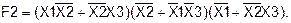
Применив вторую форму распределительного закона к 1-ой и 3-ей скобке, получим:

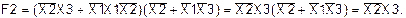
Таким образом, функции F1 и F2 тождественны.

Примечание:

Логические функции тождественны, если совпадают их минимальные формы. Если минимальные формы не совпадают, то необходимо обе функции привести к любой совершенной форме (СДНФ или СКНФ), используя правила расширения, и сравнить совершенные формы. Если они совпадают, то функции тождественны.