Линейная регрессия и корреляция.

Линейная регрессия находит широкое применение в экономет­рике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида

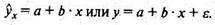
Построение линейной регрессии сводится к оценке ее пара­метров - а и b. Оценки параметров линейной регрессии могут быть найдены разными методами.

Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов(МНК). То есть, получим следующую систему нор­мальных уравнений для оценки параметров а и b:

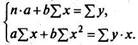
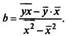
Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом оп­ределителей, найдем искомые оценки параметров а и b. Можно воспользоваться следующими готовыми формулами:

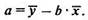
Параметр b называется коэффициентом регрессии. Его вели­чина показывает среднее изменение результата с изменением фактора на одну единицу. Формально а — значение у при x = 0.

Уравнение регрессии всегда дополняется показателем тесно­ты связи. При использовании линейной регрессии в качестве та­кого показателя выступает линейный коэффициент корреляции r_xy. Существуют разные модификации формулы линейного коэф­фициента корреляции:

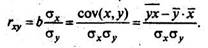
Как известно, линейный коэффициент корреляции находит­ся в границах: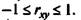

Если коэффициент регрессии b > 0, то 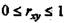, и, наоборот, при b < 0,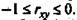

Для оценки качества подбора линейной функции рассчиты­вается квадрат линейного коэффициента корреляции r²_xy, назы­ваемый коэффициентом детерминации.

После того как найдено уравнение линейной регрессии, про­водится оценка значимости как уравнения в целом, так и отдель­ных его параметров.

Оценка значимости уравнения регрессии в целом дается с по­мощью F-критерия Фишера.

Расчетное значение критерия можно получить, используя формулу:

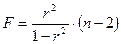
Расчетное значение сравнивается с табличным по таблицам распределения Фишера Для уровня значимости 0,05 и числа степеней свободы k1=1 и k2=n-2. Если расчетное значение больше табличного, уравнение регрессии признается значимым.

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: т_b и т_а.

Стандартная ошибка коэффициента регрессии определяется по формуле

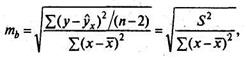
где S² — остаточная дисперсия на одну степень свободы.

Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определяется фактическое значение t-критерия Стьюдента: 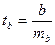, которое затем сравнивается с табличным значением при определен­ном уровне значимости α и числе степеней свободы (n - 2).

Стандартная ошибка параметра а определяется по формуле:

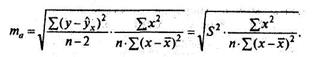
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрес­сии; вычисляется t-критерий: t_a = a/m_a, его величина сравнивается с табличным значением при df = n - 2 степенях свободы.

В прогнозных расчетах по уравнению регрессии определяется предсказываемое (у_р) значение как точечный прогноз 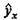при х_р =х_к, т. е. путем подстановки в уравнение регрессии 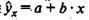соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом интегральной ошибки прогноза Е_Y, которая формируется как сумма двух ошибок: из ошибки прогноза как результата отклонения прогноза от уравнения регрессии - 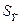и ошибки прогноза положения регрессии .

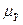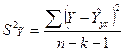
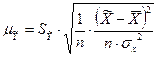
Интегральная ошибка прогноза составит:

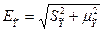
Предельная ошибка прогноза (при уровне значимости 0,05) составит:

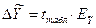
Табличное значение определили по таблице распределения Стьюдента с учетом значимости 0,05 и числом степеней свободы v = n-2.

Фактическая реализация прогноза будет находиться в доверительном интервале: 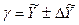. Относительная величина различий значений верхней и нижней границ характеризует точность выполненного прогноза.