Корреляция и регрессия
В практике сельскохозяйственных и биологических исследований часто возникает необходимость изучить характер связи между двумя (или более) варьирующими признаками или свойствами растений. Многие признака и свойства растений находятся между собой в определённой взаимосвязи. Некоторые из них являются взаимосвязанными, другие – изменяются в определённом направлении под влиянием общих условий. Примером связи первого типа может служить часто наблюдаемая положительная зависимость между удельной массой корневой системы в общей биомассе растений и урожайностью исследуемой зерновой культуры. С другой стороны, мощная корневая система развивается при хорошей обеспеченности растений фосфором на первых этапах их роста и развития. Таким образом, можно предположить, что фосфорные удобрения, способствуя развитию корневой системы, повлекут увеличению урожайности зерновых. А значит, между обеспеченностью растений фосфором и урожайностью будет отмечаться зависимость.
Исследование корреляции сводится к следующему.
1. Устанавливают факт зависимости изменений одного признака от изменения другого и определяют форму связи между ними. Корреляцию называют простой, если исследуется связь между двумя признаками, или множественной, когда на величину одного результативного признака влияют несколько факториальных. Как правило, в сельскохозяйственных и биологических исследованиях на результативный признак отмечается влияние нескольких факториальных, однако далеко не всегда удаётся учесть все факторы и поэтому приходиться изыскивать наиболее вероятно влияющий факториальный признак.
В зависимости от характера изменений результативного признака под влиянием факториального различают:
а) линейную корреляцию, когда с увеличением среднего значения одного признака также увеличивается среднее значение другого (прямая корреляция), или с увеличением среднего значения одного признака уменьшается среднее значение другого (обратная корреляция);
б) криволинейную корреляцию: при возрастаний значений одного признака другой возрастает неравномерно или принимает значения, возрастающие до определённой величины, а затем убывающие, или наоборот. Этот тип корреляции также бывает прямым и обратным.
2. Находят тесноту связи , то есть степень сопряжённости между значениями одного и другого признака. Степень сопряжённости обычно выражают в виде отвлечённого числа, которое при линейной корреляции называют коэффициентом корреляции, а при криволинейной зависимости – корреляционным отношением.
Линейный коэффициент корреляции.Как было сказано ранее, для характеристики линейной корреляции между двумя признаками вычисляют особый показатель коэффициент корреляции. Для того, чтобы более полно понять, что такое корреляционная зависимость, рассмотрим пример (таблица 18), по наличию связи между дозой азотного удобрения (кг д.в./га), вносимого под ячмень и содержанием белка в зерне (%)
Таблица 18
Содержание белка в зерне ярового ячменя в зависимости
от дозы азотного удобрения
| Доза азотного удобрения, кг д.в./га X | Содержание белка в зерне, % Y | Доза азотного удобрения, кг д.в./га X | Содержание белка в зерне, % Y |
| 0 (контроль, б/у) | 10,4 | 13,4 | |
| 10,2 | 13,9 | ||
| 10,9 | 13,7 | ||
| 10,4 | 13,9 | ||
| 11,9 | 14,1 | ||
| 11,5 | 14,0 | ||
| 11,5 | 14,1 | ||
| 12,8 | 14,3 | ||
| 12,3 | 14,7 | ||
| 12,9 | 14,9 | ||
| 12,8 | 14,6 | ||
| 12,8 | 14,8 | ||
| 13,2 | 14,9 | ||
| 13,7 | 15,2 | ||
| 13,3 | 15,2 |
В теоретической статистике доказывается, что коэффициент корреляции определяется индивидуальными отклонениями значений признаков от их средних значений, а соответственно обусловлен средними квадратическими отклонениями распределений. Вычисляют его несколькими способами, но классическим считается расчёт линейного коэффициента корреляции по следующей формуле:
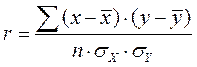 (46).
(46).
Числитель этой формулы – сумма произведений отклонений x и y от своих средних значений 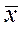 и
и 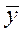 . В знаменателе
. В знаменателе 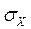 и
и 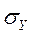 - средние квадратические отклонения распределений х и у, n – число сопоставимых пар.
- средние квадратические отклонения распределений х и у, n – число сопоставимых пар.
При отсутствии корреляции, то есть если признаки варьируют независимо друг от друга, любое из значений 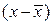 может сочетаться как с положительными, так и с отрицательными
может сочетаться как с положительными, так и с отрицательными 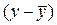 одинаково часто. Следует предпологать, что в достаточно больших совокупностях положительных произведений
одинаково часто. Следует предпологать, что в достаточно больших совокупностях положительных произведений 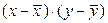 будет столько же сколько и отрицательных, и сумма произведений будет равна или почти равна нулю.
будет столько же сколько и отрицательных, и сумма произведений будет равна или почти равна нулю.
Если признаки варьируют сопряжено, то отклонения 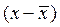 будут сочетаться не с любыми, а только с некоторыми отклонениями
будут сочетаться не с любыми, а только с некоторыми отклонениями 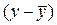 . В случае прямой корреляции положительные отклонения
. В случае прямой корреляции положительные отклонения 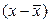 будут преимущественно сочетаться с положительными, а отрицательные
будут преимущественно сочетаться с положительными, а отрицательные 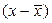 - с отрицательными
- с отрицательными 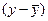 . Иначе говоря, произведение отклонений будут преимущественно однозначными и сумма их – положительной. При обратной корреляции сочетаются преимущественно отклонения с разными знаками, и сумма их произведений будет отрицательна. В том и в другом случаях сумма произведений будет тем больше, чем меньше будет независимых сочетаний отклонений, то есть чем больше будет сопряжённость между варьирующими признаками.
. Иначе говоря, произведение отклонений будут преимущественно однозначными и сумма их – положительной. При обратной корреляции сочетаются преимущественно отклонения с разными знаками, и сумма их произведений будет отрицательна. В том и в другом случаях сумма произведений будет тем больше, чем меньше будет независимых сочетаний отклонений, то есть чем больше будет сопряжённость между варьирующими признаками.
Упрощение приведённой формулы (64) математическим преобразованием даст другую формулу:
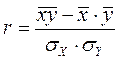 (47).
(47).
Произведя расчёт по итоговым значениям исходных переменных, линейный коэффициент корреляции можно определить, минуя вычисление средних квадратичных отклонений по формуле:
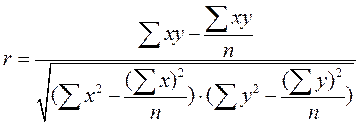 (48) или
(48) или
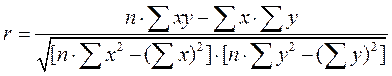 (49).
(49).
Наиболее удобной для расчётов, проводимых в условиях отсутствия достаточно мощной вычислительной техники, представляется формула 44.
Коэффициент корреляции может принимать значения от +1 до -1 в зависимости от тесноты и направленности связи.
Общепринятая степень тесноты связи отражена в таблице 30.
Таблица 19
Количественные критерии оценки тесноты связи
| Величина коэффициента корреляции | Характер связи |
| ±0–0,1 | отсутствует |
| ±0,1–0,3 | очень слабая |
| ±0,3–0,5 | слабая |
| ±0,5–0,7 | умеренная |
| ±0,7–0,9 | сильная |
| ±0,9–1,0 | очень сильная |
Если коэффициент корреляции имеет положительный знак (например, r = 0,75), то связь прямая и с увеличением значения факторного признака х увеличивается значение результативного признака у. Если r отрицательный (например, r = – 0,83), то связь обратная и с увеличением значения факторного признака х уменьшается значение результативного признака у. При r = 1,0 говорят о наличии функциональной связи между изучаемыми признаками.
Ошибка коэффициента корреляции при осуществлении выборки из нормальной совокупности рассчитывают по формуле:
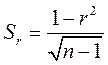 (50).
(50).
где r – коэффициент корреляции
n – выборка из генеральной совокупности (число пар (дат) наблюдений изучаемых признаков).
В классической статистике принято записывать значение коэффициента корреляции вместе с его ошибкой в виде r ± Sr. Однако, современные статистические методы предполагают определение скорректированного коэффициент корреляции, который определяется по формуле:
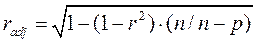 (51),
(51),
где radj – скорректированный коэффициент корреляции,
p – число параметров статистического исследования (число независимых переменных плюс 1, так как в модель включён свободный член).
При достаточно большом числе наблюдений (не менее 100) коэффициент корреляции можно считать существенным, если он превышает свою ошибку в 3 и более раза, то есть если 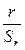 >3.
>3.
В малочисленных выборках существенность коэффициента корреляции оценивают с помощью известного критерияt. В этом случае
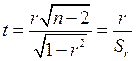 , (52)
, (52)
где n – число парных наблюдений.
Сопоставление фактического и табличного t при числе степеней свободы df = (n-2) даёт возможность оценить существенность r при избранном уровне значимости.
Дата добавления: 2021-01-26; просмотров: 690;











