ТЕМА 5. МОДЕЛИРОВАНИЕ ОДНОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ

Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят временные ряды, которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. В нем процесс экономического развития изображается в виде совокупности перерывов непрерывного позволяющих детально проанализировать особенности развития при помощи характеристик, отражающих изменения параметров экономической системы во времени.

Составными элементами ряда динамики являются показатели уровней ряда и периоды времени(годы, кварталы, месяцы, сутки) или моменты(даты) времени.

Уровни ряда обычно обозначаются через «у», моменты или периоды времени, к которым относятся уровни, - через «t».

Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:

• факторы, формирующие тенденцию ряда;

• факторы, формирующие циклические колебания ряда;

• случайные факторы.

Очевидно, что реальные данные не следуют целиком и полно­стью из каких-либо описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.

В большинстве случаев фактический уровень временного ря­да можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой вре­менной ряд представлен как сумма перечисленных компонент, называется аддитивной модельювременного ряда. Модель, в ко­торой временной ряд представлен как произведение перечислен­ных компонент, называется мультипликативной модельювремен­ного ряда. Основная задача эконометрического исследования от дельного временного ряда — выявление и придание количествен­ного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогно­зирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.

Корреляционную зависимость между последова­тельными уровнями временного ряда называют автокорреляцией уровней ряда.

Количественно ее можно измерить с помощью линейного ко­эффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени.

Одна из рабочих формул для расчета коэффициента корреля­ции имеет вид:

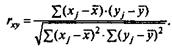
В качестве переменной xмы рассмотрим ряд у₂, у₃ ,..., y₈; в ка­честве переменной у - ряд у₁ у₂ ..., у₇. Тогда приведенная выше формула примет вид

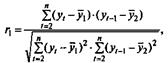
где

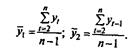
Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда t и t - 1, т. е. при лаге 1.

Аналогично можно определить коэффициенты автокорреля­ции второго и более высоких порядков. Так, коэффициент авто­корреляции второго порядка характеризует тесноту связи между уровнями у_t и y_t-₁ и определяется по формуле

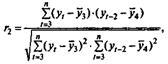
где

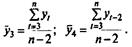
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом.С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорре­ляции, уменьшается. Некоторые авторы считают целесообраз­ным для обеспечения статистической достоверности коэффици­ентов автокорреляции использовать правило — максимальный лаг должен быть не больше (n/4).

Отметим два важных свойства коэффициента автокорреляции.Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линейной связи текущего и предыдущего уровней ряда. Поэтому по ко­эффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, па­раболу второго порядка или экспоненту), коэффициент автокор­реляции уровней исходного ряда может приближаться к нулю.

Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уров­нях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.

Последовательность коэффициентов автокорреляции уров­ней первого, второго и т. д. порядков называют автокорреляцион­ной функцией временного ряда.График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) на­зывается коррелограммой.

Анализ автокорреляционной функции и коррелограммы поз­воляет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между теку­щим и предыдущими уровнями ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограм­мы можно выявить структуру ряда.

Если наиболее высоким оказался коэффициент автокорреля­ции первого порядка, исследуемый ряд содержит только тенден­цию. Если наиболее высоким оказался коэффициент автокорре­ляции порядка τ, ряд содержит циклические колебания с перио­дичностью в τ моментов времени. Если ни один из коэффициен­тов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний и имеет структуру, сходную со структурой ряда, изображенного на рис. 5.1 в), либо ряд содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреля­ционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компонен­ты (T) и циклической (сезонной) компоненты (S).

Одним из наиболее распространенных способов моделирова­ния тенденции временного ряда является построение аналитиче­ской функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим вы­равниванием временного ряда.

Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные ви­ды функций. Для построения трендов чаще всего применяются следующие функции:

• линейный тоекд: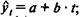

• гипербола: 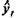= a + b/t;,

• экспоненциальный тренд: 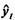= е^{а + bt1};

• тренд в форме степенной функции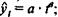

• парабола второго и более высоких порядков

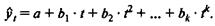
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t=1,2,..., n, а в качестве зависимой перемен­ной - фактические уровни временного ряда y_t . Для нелинейных трендов предварительно проводят стандартную процедуру их ли­неаризации.