Теорема Берри-Эссена
Однако при этом встает вопрос, при каких значениях n можно использовать нормальное приближение, а при каких – нет. Решение этого вопроса зависит от требуемой точности вычисления вероятности. Часто теорему Муавра-Лапласа применяют при выполнении условия npq > 10, а центральную предельную теорему, если np > 10.
Точный ответ на вопрос о погрешности, возникающей при замене исходного распределения нормальным, дает оценка скорости сходимости в центральной предельной теореме. Такая оценка приводится в теореме Берри-Эссена.
Теорема. Если Х1, Х2, …, Xn – независимые, одинаково распределенные случайные величины с математическим ожиданием а, дисперсией σ2 и третьим абсолютным центральным моментом μ3, то имеет место неравенство
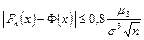 , ,
| (7.13) |
где 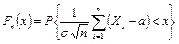 – функция распределения нормированной суммы, Ф(х)– функция распределения нормального закона с параметрами а = 0 и σ2 =1.
– функция распределения нормированной суммы, Ф(х)– функция распределения нормального закона с параметрами а = 0 и σ2 =1.
Пример 7.3. Оценить с помощью теоремы Берри-Эссена погрешность, возникающую при использовании теоремы Муавра-Лапласа.
Решение. В тереме Муавра-Лапласа распределение нормированной суммы независимых случайных величин, имеющих распределение Бернулли, заменяется нормальным.
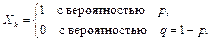
Тогда а = M(Xk) = p, σ2 = D(Xk) = pq, b = M|Xk – a|3 = pq(p2 + q2).
Применяя теорему Берри-Эссена, получаем:
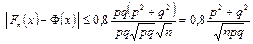 .
.
При p = q = 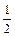 получаем
получаем 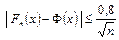 .
.
Если p = q = 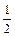 , n = 36, то |Fn(x) – Ф(x)| ≤ 0,133.
, n = 36, то |Fn(x) – Ф(x)| ≤ 0,133.
Если p = q = 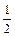 , n = 400, то |Fn(x) – Ф(x)| ≤ 0,08. ◄
, n = 400, то |Fn(x) – Ф(x)| ≤ 0,08. ◄
8. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
8.1. Понятие многомерной случайной величины
Ранее мы рассматривали случайные величины, возможные значения которой определялись одним числом. Такие величины называют одномерными. Однако часто результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин, которую называют многомерной случайной величиной или случайным вектором.
Многомерная случайная величина, случайный вектор, система случайных величин – это все различные интерпретации одного и того же математического объекта. В зависимости от удобства изложения мы будем пользоваться той или иной интерпретацией.
Так же, как и в случае одномерных случайных величин, случайные величины входящие в систему, могут быть как дискретными, так и непрерывными.
Например, успеваемость студентов вуза, которая характеризуется системой n случайных величин X1, X2, …, Xn – оценками по различным дисциплинам, проставленными в зачетной книжке – является дискретной многомерной величиной. А размер деталей, который характеризуются длиной (X), шириной (Y) и высотой (Z) – является непрерывной трехмерной величиной.
Геометрически двумерную (X, Y) и трехмерную (X, Y, Z) случайные величины можно изобразить случайной точкой плоскости Oxy или трехмерного пространства Oxyz. При этом случайные величины X, Y или X, Y, Z являются составляющими этих векторов. В случае n-мерного пространства (n > 3) также говорят о случайной точке этого пространства, хотя геометрическая интерпретация в этом случае теряет свою наглядность.
8.2. Закон распределения вероятностей
двумерной дискретной случайной величины
Так же как и для одномерной случайной величины наиболее полным, исчерпывающим описанием многомерной случайной величины является закон ее распределения. При конечном множестве возможных значений многомерной случайной величины такой закон может быть задан в виде таблицы (матрицы), содержащей все возможные сочетания значений каждой из одномерных величин, входящих в систему, и соответствующие им вероятности.
Так, если рассматривается двумерная дискретная случайная величина (X, Y), то ее двумерное распределение можно представить в виде таблицы распределения (табл. 8.1), в каждой клетке (i, j) которой располагаются вероятности произведения событий pij = P[(X = xi)(Y = yj)].
Таблица 8.1

| x1 | … | xj | … | xn | 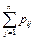
|
| y1 | p11 | … | p1j | … | p1n | p1 |
| … | … | … | … | … | … | … |
| yi | pi1 | … | pij | … | pim | pi |
| … | … | … | … | … | … | … |
| ym | pm1 | … | pmj | … | pmn | pm |
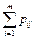
| p1 | … | pj | … | pn |
Так как события [(X = xj)(Y = yi)] (i = 1, 2, …, m; j = 1, 2, …, n), состоящие в том, что случайная величина Х примет значение xj, а случайная величина Y – значение yi, несовместны и единственно возможны, то сумма их вероятностей равна единице, т.е.
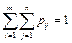 .
.
Итоговые столбцы или строки таблицы распределения (X, Y) представляют соответственно распределение одномерных составляющих (xj, pj) или (yi, pi).
Действительно, распределение одномерной случайной величины Х можно получить, вычислив вероятность события X = xj (j = 1, 2, ..., n) как сумму вероятностей несовместных событий
pj = P(X = xj) = P[(X = xj)(Y = y1) + … + (X = xj)(Y = yi) + … + (X = xj)(Y = ym)] =
= pj1 + … + pji + … + pim = 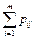 .
.
Аналогично pj = 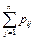 .
.
Таким образом, чтобы по таблице распределения (табл. 8.1) найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности pij из соответствующего этому значению строки (столбца) данной таблицы.
Пример 8.1. Закон распределения дискретной двумерной случайной величины (X, Y) задан в табл. 8.2. Найти законы распределения одномерных случайных величин X и Y.
| Таблица 8.2 | |||
| Y\X | |||
| 0,05 | 0,35 | 0,20 | |
| 0,15 | 0,20 | 0,05 |
Решение. Случайная величина Х может принять значения:
Х = 2 с вероятностью р1 = 0,05 + 0,15 = 0,20;
Х = 4 с вероятностью р2 = 0,35 + 0,20 = 0,55;
Х = 6 с вероятностью р2 = 0,20 + 0,05 = 0,25.
т.е. ее закон распределения
| хj | |||
| pj | 0,20 | 0,55 | 0,25 |
Аналогично закон распределения Y
| yj | ||||
| pj | 0,6 | 0,4 | ◄ |
8.3. Функция распределения многомерной случайной величины
При изучении одномерных случайных величин уже говорилось, что самой универсальной характеристикой случайной величины является функция распределения. Она существует для всех случайных величин: как дискретных, так и непрерывных. Точно также функция распределения полностью характеризует и многомерную случайную величину.
Определение. Функцией распределения n-мерной случайной величины (Х1, Х2, …, Хn) называется функция F(x1, x2, …, xn), выражающая вероятность совместного выполнения n неравенств Х1 < х1, Х2 < х2, …, Хn < xn, т.е.
| F(x1, x2, …, xn) = Р(Х1 < х1, Х2 < х2, …, Хn < xn). | (8.1) |
В случае двумерной случайной величины XY функция распределения определяется неравенством
| F(x, y) = P(X < x, Y < y). | (8.2) |
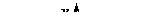 Геометрически функция распределения F(x, y) означает вероятность попадания случайной точки (X, Y) в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(x, y). Правая и верхняя границы области в квадрант не включаются – это означает, что функция непрерывна слева по каждому аргументу.
Геометрически функция распределения F(x, y) означает вероятность попадания случайной точки (X, Y) в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(x, y). Правая и верхняя границы области в квадрант не включаются – это означает, что функция непрерывна слева по каждому аргументу.
В случае двумерной дискретной случайной величины ее функция распределения определяется по формуле:
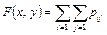 , ,
| (8.3) |
где суммирование вероятностей распространяется на все j, для которых xj < x, и все i, для которых yi < y.
Отметим свойства функции распределения двумерной случайной величины.
1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей, т.е.
| 0 ≤ F(x, y) ≤ 1. | (8.4) |
2. Функция распределения есть неубывающая функция по каждому из аргументов, т.е.
| при x2 > x1 F(x2, y) ≥ F(x1, y), при y2 > y1 F(x, y2) ≥ F(x, y1). | (8.5) |
3. Если хотя бы один из аргументов обращается в – ∞, то функция распределения равна нулю, т.е.
| F(x, – ∞) = F(– ∞, y) = F(– ∞, – ∞) = 0. | (8.6) |
4. Если один из аргументов обращается в + ∞, то функция распределения становится равной функции распределения случайной величины, соответствующей другому аргументу, т.е.
| F(x, + ∞) = F1(x), F(+ ∞, y) = F2(y), | (8.7) |
где F1(x) и F2(y) – функции распределения случайных величин X и Y, т.е.
F1(x) = P(X < x), F2(y) = P(Y < y).
5. Если оба аргумента равны + ∞, то функция распределения равна единице:
| F(+ ∞; + ∞) = 1. | (8.8) |
 Геометрически функция распределения есть некоторая поверхность, обладающая перечисленными свойствами. Для дискретной двумерной случайной величины (X, Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F(x, y).
Геометрически функция распределения есть некоторая поверхность, обладающая перечисленными свойствами. Для дискретной двумерной случайной величины (X, Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F(x, y).
Зная функцию распределения F(x, y) можно найти вероятность попадания случайной точки (X, Y) в пределы прямоугольника ABCD (рис. 8.2). Эта вероятность равна вероятности попадания в бесконечный квадрант с вершиной B(x2, y2) минус вероятность попадания в квадранты с вершинами в точках A(x1, y2) и C(x2, y1) плюс вероятность попадания в квадрант с вершиной в точке D(x1, y1) (так как эта вероятность вычиталась дважды), т.е.
| P[(x1 ≤ X < x2)(y1 ≤ Y <y2)] = F(x2, y2) – F(x1, y2) – F(x2, y1) + F(x1, y1). | (8.9) |
8.4. Плотность вероятности двумерной случайной величины
Для непрерывной двумерной случайной величины, так же как и для одномерной, существует понятие плотности вероятности.
Определение. Плотностью вероятности (или совместной плотностью) непрерывной двумерной случайной величины XY называется вторая смешанная частная производная ее функции распределения, т.е.
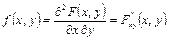 . .
| (8.10) |
 Геометрически плотность вероятности двумерной случайной величины XY представляет собой поверхность распределения в пространстве Oxyz.
Геометрически плотность вероятности двумерной случайной величины XY представляет собой поверхность распределения в пространстве Oxyz.
Отметим свойства плотности вероятности двумерной случайной величины.
1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.
f(x, y) ≥ 0.
2. Вероятность попадания непрерывной случайной величины XY в область D равна
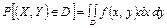 . .
| (8.11) |
3. Функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности по формуле:
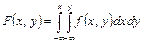 . .
| (8.12) |
4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице:
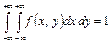 . .
| (8.13) |
Зная плотность вероятности двумерной случайной величины (X, Y) можно найти функции распределения и плотность вероятностей ее одномерных составляющих X и Y.
Так как в соответствии с (8.7) F(x, + ∞) = F1(x) и F(+ ∞, y) = F2(y), то взяв в формуле (8.12) соответственно x = + ∞ и y = + ∞, получим функции распределения одномерных случайных величин X и Y:
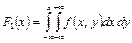 , , 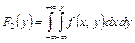 . .
| (8.14) |
Дифференцируя функции распределения F1(x) и F2(y) соответственно по аргументам x и y, получим плотности вероятности одномерных случайных величин X и Y:
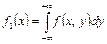 , , 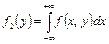 , ,
| (8.15) |
т.е. несобственный интеграл в бесконечных пределах от совместной плотности двумерной случайной величины по аргументу x дает плотность вероятности f2(y), а по аргументу y – плотность вероятности f1(x).
8.5. Условные законы распределения двумерной случайной величины
Итак, мы выяснили, как по известному закону распределения системы двух случайных величин определить законы распределения одномерных величин, входящих в систему.
Естественно возникает вопрос: нельзя ли по законам распределения одномерных величин, входящих в систему, найти закон распределения системы в целом? Оказывается, в общем случае этого сделать нельзя. Для того, чтобы полностью описать систему случайных величин, недостаточно знать распределение каждой из ее составляющих. Нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью условных законов распределения.
Определение. Условным законом распределения одной из одномерных составляющих двумерной случайной величины XY называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в определенный интервал).
Для дискретных случайных величин условные вероятности находятся по формулам:
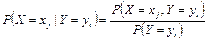 или или 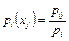 . .
| (8.16) |
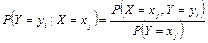 или или 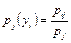 . .
| (8.17) |
В случае непрерывных случайных величин необходимо определить плотность вероятности условных распределений. Заменяя в формулах для дискретных величин вероятности событий «элементами вероятностей», получим:
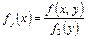 , , 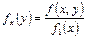 . .
| (8.18) |
т.е. условная плотность вероятности одной из одномерных составляющих двумерной случайной величины равно отношению ее совместной плотности к плотности вероятности другой составляющей.
Пример 8.2. По данным примера 8.1 найти условный закон распределения составляющей Х при условии, сто составляющая Y приняла значение y1 =1.
Решение. Искомый закон определяется следующей совокупностью условных вероятностей:
p(x1 | y1), p(x2 | y1), p(x3 | y1).
Воспользовавшись формулой (8.16) и учитывая, что p(y1) = 0,6 (пример 8.1), получаем:
p(x1 | y1) = 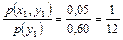 ; p(x2 | y1) =
; p(x2 | y1) = 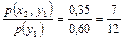 ;
;
p(x3 | y1) = 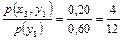 .◄
.◄
Важной характеристикой условного распределения вероятностей является условное математическое ожидание.
Условным математическим ожиданием дискретной случайной величины Y при Х = х (х – определенное возможное значение Х) называют произведение возможных значений Y на их условные вероятности:
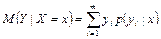 . .
| (8.19) |
Для непрерывных величин
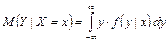 . .
| (8.20) |
Аналогично определяется условное математическое ожидание случайной величины Х.
Пример 8.3. По данным примера 8.1 найти условное математическое ожидание составляющей Y при условии, что составляющая Х примет значение х1 = 2.
Решение. Найдем р(х1), для чего сложим вероятности, помещенные в первом столбце табл. 8.2
р(х1) = 0,05 + 0,15 = 0,2.
Найдем условное распределение вероятностей величины Y при при Х = х1 =3:
p(y1 | x1) = 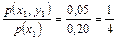 ; p(y2 | x1) =
; p(y2 | x1) = 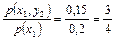 .
.
Найдем условное математическое ожидание по формуле (8.19):
M(Y | X = x1) = 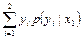 = y1·p(y1 | x1) + y2·p(y2 | x1) =
= y1·p(y1 | x1) + y2·p(y2 | x1) = 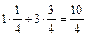 = 2,5. ◄
= 2,5. ◄
Условное математическое ожидание случайной величины Y при Х = х, т.е. Mx(Y), есть функция от х, называемая функцией регрессии или просто регрессией Y по Х. Аналогично My(X) называется функцией регрессии или регрессией X по Y. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессии) Y по Х и Х по Y.
8.6. Зависимые и независимые случайные величины
Ранее мы назвали две случайные величины независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Теперь можно дать общее определение независимости случайных величин, основанное на независимости событий X < x и Y < y, т.е. функций распределения F1(x) и F2(y).
Определение. Случайные величины X и Y называются независимыми, если их совместная функция распределения F(x, y) представляется в виде произведения функций F1(x) и F2(y) этих случайных величин, т.е.
| F(x, y) = F1(x)·F2(y). | (8.21) |
При невыполнении этого равенства случайные величины называются зависимыми.
Дифференцируя дважды равенство (8.19) по аргументам x и y, получим
| f(x, y) = f1(x)·f2(y), | (8.22) |
т.е. для независимых непрерывных случайных величин их совместная плотность равна произведению плотностей вероятностей этих случайных величин. Другими словами, независимость двух случайных величин, что условные вероятности каждой из них совпадают с соответствующими безусловными плотностями вероятностей.
8.7. Числовые характеристики двумерной случайной величины.
Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, используются и другие характеристики, к числу которых относятся ковариация и коэффициент корреляции.
Определение. Ковариацией (или корреляционным моментом) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.
| Kxy = M[(X – M(X))(Y – M(Y))] | (8.23) |
или Kxy = M[(X – ax)(Y – ay)],
где ax = M(X), ay = M(Y).
Из определения следует, что Kxy = Kyx.
Для дискретных случайных величин
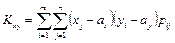 . .
| (8.24) |
Для непрерывных случайных величин
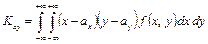 . .
| (8.25) |
Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки (ax, ay).
Отметим свойства ковариации:
1. Ковариация двух независимых случайных величин равна нулю.
2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е.
| Kxy = M(XY) – M(X)·M(Y) = M(XY) – axay. | (8.26) |
3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е.
| │Kxy│≤ σxσy. | (8.27) |
Не трудно заметить, что ковариация имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина ковариации зависит от единиц измерения случайных величин. Такая особенность затрудняет сравнение ковариаций различных систем случайных величин. Для устранения этого недостатка вводится безразмерная характеристика – коэффициент корреляции.
Определение. Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отношений этих величин, т.е.
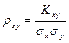 . .
| (8.28) |
Из определения следует, что ρxy = ρyx.
Отметим свойства коэффициента корреляции.
1. Коэффициент корреляции принимает значения на отрезке [–1; 1], т.е.
| –1 ≤ ρ ≤ 1. | (8.29) |
2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. ρ = 0.
3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.
Пример 8.4. По данным примера 8.1 определить ковариацию и корреляционный момент случайных величин Х и Y.
Решение. В примере 8.1 были получены следующие распределения одномерных случайных величин
| X: | хj | |||
| pj | 0,20 | 0,55 | 0,25 |
| Y: | yj | ||
| pj | 0,60 | 0,40 |
Найдем математические ожидания и средние квадратические отклонения этих случайных величин:
ах = М(Х) = 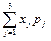 = 2·0,20 + 4·0,55 + 6·0,25 = 4,1;
= 2·0,20 + 4·0,55 + 6·0,25 = 4,1;
М(Х2) = 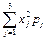 = (22·0,20 + 42·0,55 + 62·0,25 = 18,6;
= (22·0,20 + 42·0,55 + 62·0,25 = 18,6;
D(X) = M(X2) – M(X)2 = 18,6 – 4,12 = 1,79; 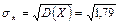 ≈ 1,34.
≈ 1,34.
аy = М(y) = 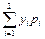 = 1·0,60 + 3·0,40 = 1,8;
= 1·0,60 + 3·0,40 = 1,8;
М(Y2) = 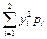 = (12·0,60 + 32·0,40 = 4,2;
= (12·0,60 + 32·0,40 = 4,2;
D(Y) = M(Y2) – M(Y)2 = 4,2 – 1,82 = 0,96; 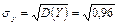 ≈ 0,98.
≈ 0,98.
Для нахождения математического ожидания M(XY) произведения случайных величин Х и Y можно составить закон распределения произведения двух дискретных случайных величин, а затем по нему найти M(XY). Однако M(XY) можно найти непосредственно по табл. 8.2 распределения двумерной случайной величины (X, Y) по формуле:
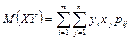 ,
,
где двойная сумма означает суммирование по всем mn клеткам таблицы (m – число строк, n – число столбцов):
M(XY) = (1·2·0,05 + 1·4·0,35 + 1·6·0,20) + (3·2·0,15 + 3·4·0,20 + 3·6·0,05) = 6,9.
Вычисляем ковариацию по формуле (8.26):
Kxy = M(XY) – M(X)M(Y) = 6,9 - 4,1·1,8 = - 0,48.
Вычисляем коэффициент корреляции по формуле (8.28):
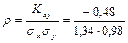 = - 0,37,
= - 0,37,
т.е. между случайными величинами Х и Y существует отрицательная линейная зависимость ◄
Дата добавления: 2021-12-14; просмотров: 425;











