Центральная предельная теорема
Рассмотренный закон больших чисел устанавливает факт приближения средней большого числа случайных величин к определенным постоянным. Но этим не ограничиваются закономерности, возникающие в результате суммарного действия случайных величин. Оказывается, что при некоторых условиях совокупное действие случайных приводит к определенному, а именно – к нормальному закону распределения.
Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.
Теорема Ляпунова
Теорема. Если Х1, Х2, …, Хn – независимые случайные величины, у каждой из которых существует математическое ожидание М(Хi) = а, дисперсия D(Хi) = σ2, абсолютный центральный момент третьего порядка 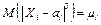 и выполняется условие
и выполняется условие
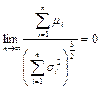 , ,
| (7.12) |
то закон распределения суммы Y = Х1 + Х2 + … + Хn при n → ∞ неограниченно приближается к нормальному с математическим ожиданием 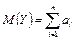 и дисперсией
и дисперсией 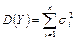 .
.
Смысл условия (7.12) состоит в том, чтобы в сумме 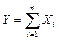 не было слагаемых, влияние которых на рассеяние суммарной величины Y подавляюще велико по сравнению с влиянием остальных. Также не должно быть большого числа случайных слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных. Таким образом, удельный вес каждого отдельного слагаемого должен стремиться к нулю при увеличении числа слагаемых.
не было слагаемых, влияние которых на рассеяние суммарной величины Y подавляюще велико по сравнению с влиянием остальных. Также не должно быть большого числа случайных слагаемых, влияние которых очень мало по сравнению с суммарным влиянием остальных. Таким образом, удельный вес каждого отдельного слагаемого должен стремиться к нулю при увеличении числа слагаемых.
Следствие. Если Х1, Х2, …, Хn – независимые случайные величины, у которых существуют равные математические ожидания М(Хi) = а, дисперсии D(Хi) = σ2 и абсолютные центральные моменты третьего порядка 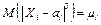 , то закон распределения суммы Y = Х1 + Х2 + … + Хn при n → ∞ неограниченно приближается к нормальному с математическим ожиданием
, то закон распределения суммы Y = Х1 + Х2 + … + Хn при n → ∞ неограниченно приближается к нормальному с математическим ожиданием 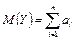 и дисперсией
и дисперсией 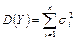 .
.
В частности, если все случайные величины распределены одинаково, то закон распределения их суммы неограниченно приближается к нормальному закону при n → ∞.
Дата добавления: 2021-12-14; просмотров: 437;











