Физическая роль маховика в машине
Физическую роль маховика в машине можно представить себе следующим образом. Если в пределах некоторого угла поворота начального звена механизма работа движущих сил больше работы сил сопротивления, то начальное звено вращается ускоренно и кинетическая энергия механизма увеличивается.
При отсутствии маховика весь прирост кинетической энергии распределяется между массами звеньев механизма. Маховик увеличивает общую массу механизма и поэтому при том же увеличении кинетической энергии прирост угловой скорости без маховика будет больше, чем при наличии маховика.
Итак, маховик является аккумулятором кинетической энергии, расходующим ее, когда работа сил сопротивления больше работы сил движущих.
Маховик выполняют в форме сплошного диска или шкива со спицами и массивным ободом и укрепляют на валу машины. Особенно большое значение имеет установка маховика для машин, работающих с резко возрастающей нагрузкой (пресса, дробилки, прокатные станы). В данных машинах накопленная маховиком энергия используется для преодоления повышенных полезных нагрузок без увеличения мощности двигателя.
Определение момента инерции маховика при 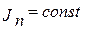 .
.
Задача об удержании скорости ведущего звена в заранее заданных пределах 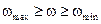 может быть решена с помощью постановки на одно из звеньев машины, совершающих вращательное движение, диска с необходимым (расчетным) моментом инерции.
может быть решена с помощью постановки на одно из звеньев машины, совершающих вращательное движение, диска с необходимым (расчетным) моментом инерции.
Пусть задано δ, ωcp, 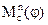 (φ) и
(φ) и 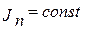
Последнее означает, что движение всех звеньев связано с движением ведущего звена механизма постоянным передаточным отношением.
Требуется определить такой момент инерции маховика 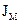 , чтобы скорости ведущего звена не выходили за пределы ωmax и ωmin, которые определяются по формуле:
, чтобы скорости ведущего звена не выходили за пределы ωmax и ωmin, которые определяются по формуле:
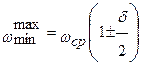
В случае, когда 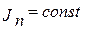 эти значения угловой скорости будут соответствовать положениям звена приведения, когда кинетическая энергия механизма будет принимать экстремальные значения, что в общем случае не имеет места при
эти значения угловой скорости будут соответствовать положениям звена приведения, когда кинетическая энергия механизма будет принимать экстремальные значения, что в общем случае не имеет места при 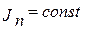 .
.
Отметим, что случай 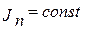 в известном смысле распространяется и на случай, если
в известном смысле распространяется и на случай, если 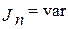 . Дело в том, что методах Мерцалова и Гутьяра прежде, чем рассчитать момент инерции маховика, его кинетическая энергия выделяется из кинетической энергии машины и таким образом задача сводится к определению момента инерции маховика для системы с
. Дело в том, что методах Мерцалова и Гутьяра прежде, чем рассчитать момент инерции маховика, его кинетическая энергия выделяется из кинетической энергии машины и таким образом задача сводится к определению момента инерции маховика для системы с 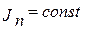 .
.
Получим уравнение, с помощью которого можно определить JM механизма, удовлетворяющий постоянному условию.
В случае 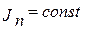 ,
, 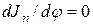 и дифференциальное уравнение движения машины принимает вид:
и дифференциальное уравнение движения машины принимает вид:
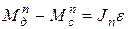
и т. к.
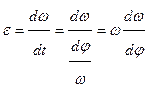
 ,
,
то, обозначив 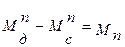 ,
,
будем иметь 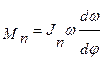
Интегрируя это уравнение на участке углов поворота звена приведения от 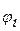 до
до 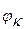 , будем иметь:
, будем иметь:
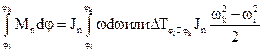
| (4.22) |
Так, как полученное равенство справедливо для любых значений угла поворота главного вала, то выберем углы поворота 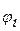 и
и 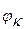 так, чтобы они соответствовали экстремальным значениям угловых скоростей звена приведения. Пусть
так, чтобы они соответствовали экстремальным значениям угловых скоростей звена приведения. Пусть 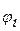 соответствует
соответствует 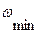 , а
, а 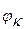 -
- 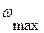 . Тогда
. Тогда 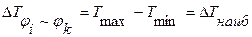 представит наибольший перепад кинетической энергии машины за цикл и уравнение (*) запишется так:
представит наибольший перепад кинетической энергии машины за цикл и уравнение (*) запишется так:
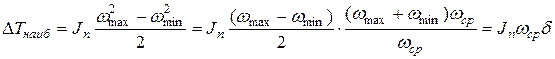
откуда
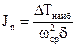
| (4.23) |
По этой формуле может быть определен приведенный момент инерции механизма при заданной нагрузке, ωср и δ. Как видим, для совершенно равномерного движения звена приведения (δ=0) 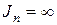 .
.
Заметим, что вид этой формулы сохраняется и в том случае, если 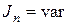 , т. к. из кинетической энергии механизма выделяется
, т. к. из кинетической энергии механизма выделяется
кинетическая энергия маховика, у которого 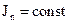 и тогда
и тогда 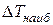 будет отнесено к маховику. Можно так же показать, что при одной и той же нагрузке потеря скорости звена приведения будет тем меньше, чем больше момент инерции звена приведения:
будет отнесено к маховику. Можно так же показать, что при одной и той же нагрузке потеря скорости звена приведения будет тем меньше, чем больше момент инерции звена приведения:
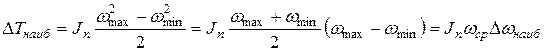
откуда
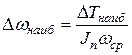
Эта зависимость оправдывает наше утверждение, т. е. чем больше инерционность механизма, тем меньше потери скорости. Заданного значения δ добиваются путем постановки на одно из вращающихся звеньев механизма маховика с требуемым приведенным к звену приведения моментом инерции, который вычисляется из условия:
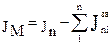 ,
,
где: 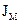 - приведенный к звену приведения момент инерции маховика;
- приведенный к звену приведения момент инерции маховика;
 - сумма приведенных к звену приведения моментов инерции всех звеньев механизма (без маховика);
- сумма приведенных к звену приведения моментов инерции всех звеньев механизма (без маховика);
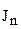 - расчетный приведенный момент инерции звена приведения, вычисленный по формуле (4.23).
- расчетный приведенный момент инерции звена приведения, вычисленный по формуле (4.23).
Обычно нагрузка на машину задается в виде графика приведенных моментов сил сопротивления и по этой нагрузке подбирается соответствующий двигатель, момент которого задается в виде графика приведенных к звену приведения движущих сил. Интегрируя эти графики на протяжении одного цикла, получают работу сил движущих и сил сопротивления за цикл (рис. 4.8). Для установившегося движения (Ад) цикла = (Ас) цикла – это является основным условием установившегося движения и служит основанием для определения мощности двигателя.
|
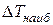 и подставляют в формулу (4.23).
и подставляют в формулу (4.23).
Отметим, что операцию вычитания можно произвести сразу на графике моментов и, минуя при этом график работ, получить график ∆Т (φ). Это следует из того, что интеграл суммы равен сумме интегралов.
Как видим, 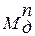 и
и 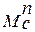 имеют не одинаковые значения в различных положениях механизма. Маховик накапливает кинетическую энергию на участках цикла, где
имеют не одинаковые значения в различных положениях механизма. Маховик накапливает кинетическую энергию на участках цикла, где 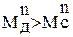 и поэтому скорость звена приведения возрастает. На участках же, где
и поэтому скорость звена приведения возрастает. На участках же, где 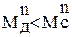 , маховик и другие звенья механизма отдают кинетическую энергию, снижая скорость, и дополняют момент движущих сил до равенства с моментом сил сопротивления за счет инерционного момента сил тормозящихся масс. Таким образом, маховик выполняет роль аккумулятора кинетической энергии, который накапливает и отдает ее в соответствующих положениях механизма, снижая потерю скорости звена приведения.
, маховик и другие звенья механизма отдают кинетическую энергию, снижая скорость, и дополняют момент движущих сил до равенства с моментом сил сопротивления за счет инерционного момента сил тормозящихся масс. Таким образом, маховик выполняет роль аккумулятора кинетической энергии, который накапливает и отдает ее в соответствующих положениях механизма, снижая потерю скорости звена приведения.
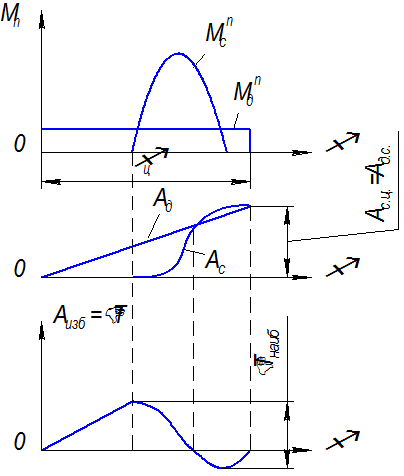
Рис. 4.8
Отметим следующее:
1. Для определения 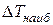 нет необходимости иметь график полной кинетической энергии машины. Достаточно иметь график ее приращений.
нет необходимости иметь график полной кинетической энергии машины. Достаточно иметь график ее приращений.
2. Нет необходимости вычислять предельные скорости 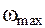 и
и 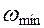 кроме отдельных специальных случаев, когда по ним определяется δ (например определения δ, если машина приводится от асинхронного двигателя).
кроме отдельных специальных случаев, когда по ним определяется δ (например определения δ, если машина приводится от асинхронного двигателя).
3. При постоянном приведенном моменте инерции механизма и постоянной нагрузке ∆T=0 при любом φ, в этом случае маховик не нужен.
4. После того, как найден 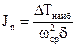 , можно построить график полной кинетической энергии машины T(φ) (рис. 4.9) и, следовательно могут быть определены действительные угловые скорости звена приведения в любом положении механизма. Положение оси абсцисс графика полной кинетической энергии машины определяется из тех соображений, что известны значения полной кинетической энергии при экстремальных значениях угловых скоростей звена приведения:
, можно построить график полной кинетической энергии машины T(φ) (рис. 4.9) и, следовательно могут быть определены действительные угловые скорости звена приведения в любом положении механизма. Положение оси абсцисс графика полной кинетической энергии машины определяется из тех соображений, что известны значения полной кинетической энергии при экстремальных значениях угловых скоростей звена приведения:
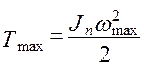 ;
; 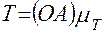 ,
,
откуда 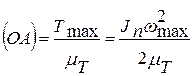
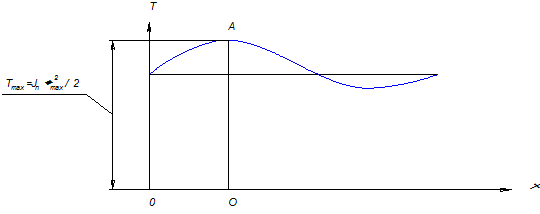
Рис. 4.9
.
5. Форма кривой графика Т(φ) определяется внешними силами, действующими на механизм, и при отсутствии последних будет представлена прямой параллельной оси абсцисс для любого механизма независимо от его структуры, как при 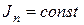 , так и при
, так и при 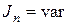 .
.
Как отмечалось выше, задача об удержании скорости ведущего звена машины в заранее заданных пределах 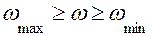 может быть решена с помощью постановки на одно из звеньев, совершающих вращательное движение, маховика с необходимым моментом инерции.
может быть решена с помощью постановки на одно из звеньев, совершающих вращательное движение, маховика с необходимым моментом инерции.
Покажем, как рассчитать δ для асинхронного двигателя.
Из технического задания на проектирование машины обычно бывают известными: производительность машины, механическая характеристика силы сопротивления и тип двигателя.
В подавляющем большинстве случаев в качестве двигателя принимается асинхронный электродвигатель как наиболее простой и дешевый.
По заданной производительности машины рассчитывается средняя угловая скорость 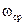 главного вала машины, а затем определяется работа силы сопротивления за цикл и мощность двигателя:
главного вала машины, а затем определяется работа силы сопротивления за цикл и мощность двигателя:
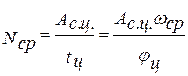
После того, как проведен энергетический расчет машины и определена мощность электродвигателя, производится расчет момента инерции маховика. Для привода проектируемой машины по каталогу можно выбрать электродвигатели различных типов с одной и той же мощностью. Например, для привода машин с неравномерной и пиковой нагрузками применяются электродвигатели типов АО и АОС. Покажем, как выбор того или иного типа электродвигателя влияет на величину коэффициента неравномерности движения машины, а следовательно на размеры ее маховика.
Исходя из данных механической характеристики асинхронного электродвигателя (рис. 4.10), можно установить математическую связь между номинальным скольжением ротора электродвигателя и коэффициентом неравномерности движения машины.
С достаточной для практики точностью можно принять, что устойчивая часть механической характеристики асинхронных двигателей прямолинейна, тогда (рис. 4.9) из подобия треугольников имеем:
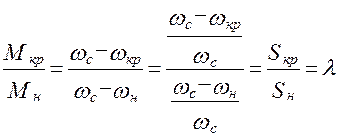
где: 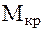 - критический момент, при котором двигатель переходит на неустойчивую часть механической характеристики;
- критический момент, при котором двигатель переходит на неустойчивую часть механической характеристики;
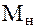 - номинальный момент на валу электродвигателя;
- номинальный момент на валу электродвигателя;
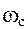 - синхронная угловая скорость ротора электродвигателя;
- синхронная угловая скорость ротора электродвигателя;
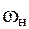 - номинальная угловая скорость электродвигателя;
- номинальная угловая скорость электродвигателя;
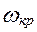 - критическая угловая скорость ротора электродвигателя;
- критическая угловая скорость ротора электродвигателя;
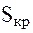 - критическое скольжение ротора электродвигателя,
- критическое скольжение ротора электродвигателя,
определяемое равенством:
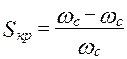 ,
,
где 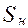 - номинальное скольжение ротора электродвигателя,
- номинальное скольжение ротора электродвигателя,
определяемое равенством:
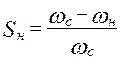
λ- коэффициент опрокидывания.
Из таблицы технических данных асинхронных электродвигателей с короткозамкнутым ротором общего назначения следует, что для двигателей типа АО (электродвигатели в закрытом обдуваемом исполнении) с синхронным числом оборотов ротора, равным 1000 об/мин, коэффициент опрокидывания колеблется в пределах λ=1,8…2,2, а для двигателей АОС (электродвигатели с повышенным скольжением в закрытом обдуваемом исполнении) при том же значении синхронных чисел оборотов коэффициент опрокидывания лежит в пределах: λ=2,2…2,6.
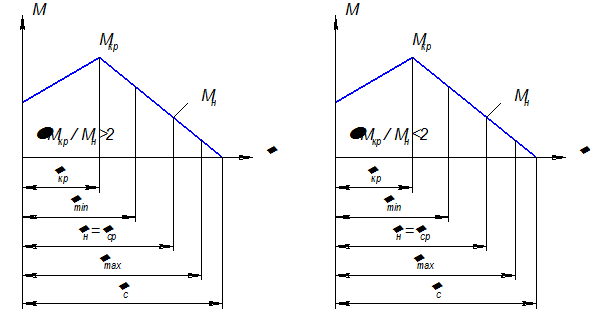
Рис. 4.10
В соответствии с этим рассмотрим два случая, предварительно заметив, что в качестве средней угловой скорости принята номинальная угловая скорость ротора электродвигателя и предельные значения угловых скоростей ротора 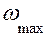 и
и 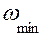 поэтому должны симметрично располагаться по отношению к его номинальной угловой скорости
поэтому должны симметрично располагаться по отношению к его номинальной угловой скорости 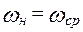
Случай 1. Этот случай соответствует, когда коэффициент 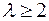 , тогда
, тогда 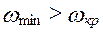 , а максимальное значение угловой скорости принимаем равным синхронной угловой скорости. Исходя из этих соображений, находим предельные угловые скорости ротора:
, а максимальное значение угловой скорости принимаем равным синхронной угловой скорости. Исходя из этих соображений, находим предельные угловые скорости ротора:
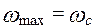 ,
,
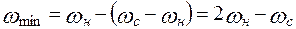
Далее определяем коэффициент неравномерности движения машины:
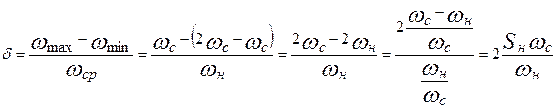
И так: 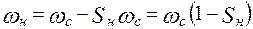 , то
, то
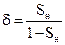
| (4.23) |
Случай 2. Этот случай соответствует коэффициенту опрокидывания λ<2, тогда 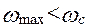 , а минимальное значение угловой скорости принимаем равной критической угловой скорости ротора. Как и прежде, находим предельные значения угловых скоростей ротора:
, а минимальное значение угловой скорости принимаем равной критической угловой скорости ротора. Как и прежде, находим предельные значения угловых скоростей ротора:
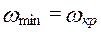
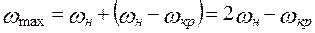
Далее определяем коэффициент неравномерности движения машины: 
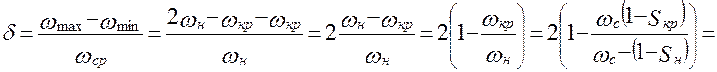
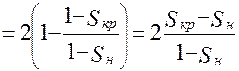
Итак,
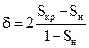
| (4.24) |
Полученные в обоих случаях δ являются одновременно и критическими значениями.
В качестве примера возьмем два электродвигателя одинаковой мощности и с одинаковыми синхронными числами оборотов ротора, но разных типов: двигатель типа АО мощностью 40 квт и синхронным числом оборотов ротора, равным 1000 об/мин и двигатель типа АОС с теми же показателями. Для обоих двигателей коэффициент опрокидывания 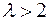 , поэтому коэффициент неравномерности движения вычисляем по формуле (4.23). Для двигателя типа АО получим δ=0,0204; а для типа двигателя АОС δ=0,087.
, поэтому коэффициент неравномерности движения вычисляем по формуле (4.23). Для двигателя типа АО получим δ=0,0204; а для типа двигателя АОС δ=0,087.
Рассматривая эти результаты, видим, что при всех прочих равных условиях момент инерции маховика, работающего с двигателем типа АО должен быть в 4,3 раза больше момента инерции маховика, работающего с двигателем типа АОС.
Надо иметь в виду, что двигатель никогда не доведет угловую скорость маховика до значения, соответствующего синхронной скорости ротора, т. к. в машине всегда присутствуют вредные сопротивления (трение, гидравлические сопротивления смазки, сопротивление воздуха и т. п.). В силу этих причин 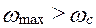 и при определении δ следует всегда вводить на это некоторую поправку. Кроме того, нельзя доводить значение ωmin до критической скорости и поэтому должно иметь место следующее соотношение: ωкр<ωmin.
и при определении δ следует всегда вводить на это некоторую поправку. Кроме того, нельзя доводить значение ωmin до критической скорости и поэтому должно иметь место следующее соотношение: ωкр<ωmin.
Таблица 2. Технические данные асинхронных электродвигателей с короткозамкнутым ротором общего назначения. Синхронное число оборотов ротора 1500 об/мин.
| Тип АО – электродвигатели в закрытом обдуваемом исполнении | Тип АОС - электродвигатели с повышенным скольжением в закрытом обдуваемом исполнении | |||||
| Номинальная мощность квт | Номинальное число оборотов ротора об/мин | Коэффициент опрокидывания | Номинальное скольжение | Номинальное число оборотов ротора об/мин | Коэффициент опрокидывания | Номинальное скольжение |
| 1,0 | 2,0 | 0,060 | 2,3 | 0,133 | ||
| 1,7 | 2,0 | 0,053 | 2,3 | 0,133 | ||
| 2,8 | 2,0 | 0,053 | 2,3 | 0,133 | ||
| 4,5 | 2,0 | 0,040 | 2,3 | 0,110 | ||
| 7,0 | 2,0 | 0,040 | 2,3 | 0,110 | ||
| 2,3 | 0,027 | 2,5 | 0,100 | |||
| 2,3 | 0,027 | 2,5 | 0,100 | |||
| 2,3 | 0,027 | 2,5 | 0,100 | |||
| 2,3 | 0,027 | 2,6 | 0,090 | |||
| 2,3 | 0,020 | 2,6 | 0,080 | |||
| 2,3 | 0,020 | 2,6 | 0,070 | |||
| 2,3 | 0,020 | 2,6 | 0,070 | |||
| 2,3 | 0,020 | 2,6 | 0,070 |
Определение угловой скорости главного звена при заданном приведенном моменте.
Пусть для машины задан закон изменения приведенного момента
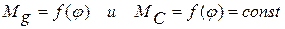
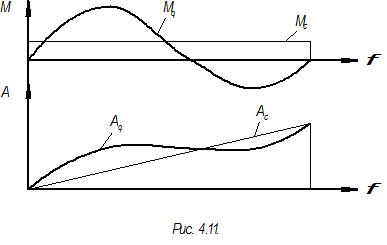
Согласно закону сил изменение кинетической энергии механизма равно работе внешних сил
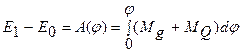
| (4.25) |
где Е0 – кинетическая энергия механизма в начальный момент,
A(φ) – работа внешних сил, произведенная внешними силами движущими и силами сопротивления за время поворота начального звена на угол φ.
После построения диаграммы избыточного момента нетрудно построить диаграмму изменения кинетической энергии
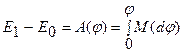
Интегральную кривую можно построить методом графического интегрирования
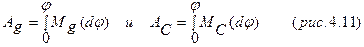
Работа 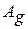 есть площадь между кривой
есть площадь между кривой 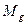 и осью
и осью 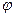 .
.
Работа 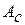 есть площадь между кривой
есть площадь между кривой 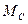 и осью
и осью 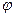 :
:
E2-E1=Ag-Ac
Для нахождения реальной угловой скорости главного звена используем уравнение 8.
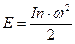
откуда
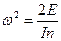
| (4.26) |
Строим в масштабе 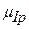 диаграмму приведенного момента инерции
диаграмму приведенного момента инерции 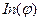 (Рис. 4.12)
(Рис. 4.12)
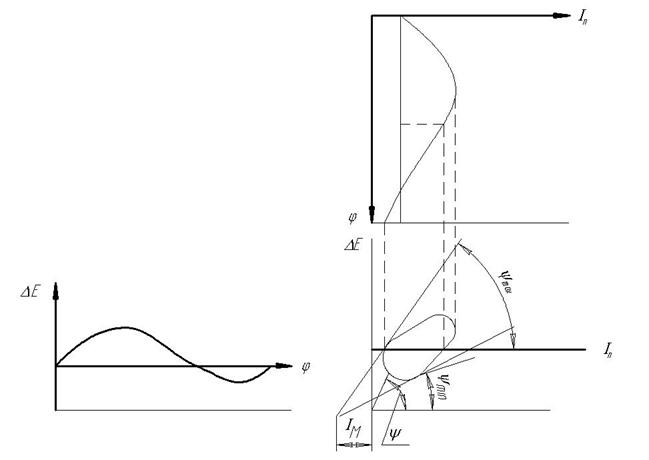
Рис. 4.12
Построением добиваемся исключения параметра 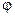 .Получаем замкнутую кривую
.Получаем замкнутую кривую 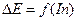 .
.
Отметим произвольную точку К и соединим ее с началом координат
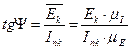
| (4.27) |
Из уравнений (4.26) и (4.27)
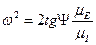
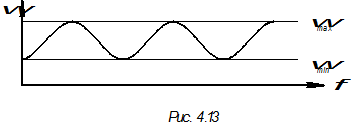
Подсчитав для каждого положения 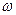 можно построить график
можно построить график 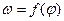 (рис. 4.13)
(рис. 4.13)
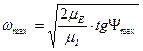
| (4.28) |
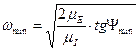
| (4.29) |
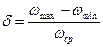
| (4.30) |
Отсюда
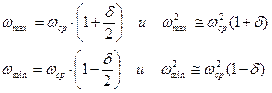
Такое допущение можно сделать, так как 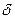 – очень мало.
– очень мало.
Тогда
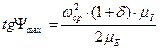
| (4.31) | |
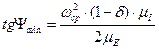
| (4.32) |
При заданных 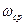 и
и 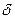 можно определить
можно определить 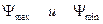 .
.
Если при этом уже построены диаграммы 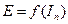 , то можно определить дополнительный момент инерции, который необходимо добавить к механизму с целью получения механизма с лучшим коэффициентом неравномерности.
, то можно определить дополнительный момент инерции, который необходимо добавить к механизму с целью получения механизма с лучшим коэффициентом неравномерности.
Под углами 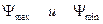 проводим лучи касательно к кривой
проводим лучи касательно к кривой 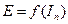 . В точке пересечения этих лучей получим новую систему координат с новым значением
. В точке пересечения этих лучей получим новую систему координат с новым значением 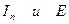 .
.
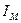 – приведенный момент инерции маховика.
– приведенный момент инерции маховика.
Определение момента инерции маховика в случае, когда 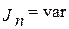
Трудность решения задачи о маховике в этом случае заключается в том, что положения механизма с экстремальными значениями кинетической энергии и угловых скоростей в общем случае не совпадают и, следовательно, нет основания полагать, что наибольшему перепаду энергии 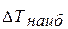 , соответствуют положения звена приведения, где имеют место ωmax и ωmin, тогда
, соответствуют положения звена приведения, где имеют место ωmax и ωmin, тогда 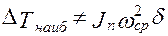 , как это было при
, как это было при 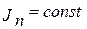
Тогда, представляя приведенный момент инерции состоящим из постоянной и переменной частей, запишем:
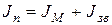 ,
,
где 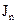 - приведенный момент инерции механизма;
- приведенный момент инерции механизма;
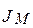 - приведенный момент инерции маховика;
- приведенный момент инерции маховика;
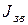 - приведенный момент инерции звеньев, движение которых связано с движением звена приведения переменным передаточным отношением (т. е. звеньев, направления движений которых изменяются).
- приведенный момент инерции звеньев, движение которых связано с движением звена приведения переменным передаточным отношением (т. е. звеньев, направления движений которых изменяются).
Заметим, что кинетическая энергия маховика будет иметь экстремальные значения в тех же положениях звена приведения, где будут иметь место экстремальные значения его угловой скорости;
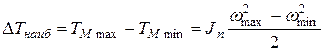
(где индекс М означает принадлежность к маховику).
Поэтому, если из кинетической энергии машины выделить кинетическую энергию маховика ТМ, то можно определить наибольший перепад его энергии, а затем определить и его необходимый момент инерции тем же методом, как это делалось для машин с 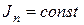 .
.
Интегральные методы расчета маховика, основанные на решении уравнения движения машины, представленного в виде закона изменения кинетической энергии, отличаются друг от друга способами определения наибольшего перепада энергии маховика 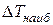 .
.
Здесь существуют принципиально точные методы расчета без использования каких- либо упрощенных предположений и приближенные методы, использующие эти предположения.
Дата добавления: 2021-12-14; просмотров: 713;











