Метод Гутьяра Б.М. (точный метод)

Этот метод был предложен в 1939 году. Ход рассуждений, касающийся Мерцалова, применим и в методе Гутьяра, однако из графика ∆Т(φ) будем вычитать энергию звеньев, вычисленную по формуле:

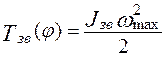, тогда

.

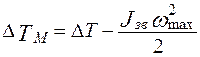Очевидно, что в этом случае мы вычитаем завышенные по абсолютной величине значения ординат графика Тзв(φ), т. к. из ∆Т(φ) мы вычитаем величины больше чем следует по отношению к истинному значению ординат, которые получились бы, если бы мы вычитали:

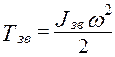
где ω – истинное значение угловой скорости звена приведения.

Определим на сколько завышены по абсолютной величине ординаты графика ∆ТМ(φ).

Нам следовало вычитать:

,

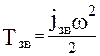а мы вычитаем

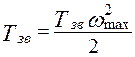
следовательно, в каждом положении нами внесена ошибка

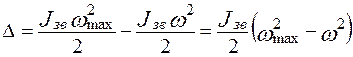
выносится за скобки т. к. это приведенный момент инерции звеньев в одном и том же положении.

Однако в положении звена приведения, где 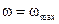, ошибка ∆=0. Значит, в этом положении мы имеем истинное значение ∆Т_М. Этому положению соответствует:

.

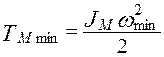В результате построения кривых 1 и 2 (рис. 4.15), получим точки А и В, соответствующие максимуму и минимуму кинетической энергии маховика Т_Мmax и Т_Мmin.

Имея эти точки А и В на графике, находим точное значение наибольшего перепада кинетической энергии маховика ∆ТМ наиб и вычисляем момент инерции маховика:

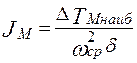
Рис. 4.15

Примечание 1: Все ординаты графиков в одном и том же положении механизма

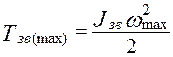и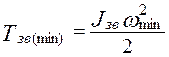

связаны зависимостью:

.

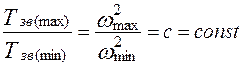Примечание 2: Учитывая пункт 1 примечания можно строить только одну кривую, например Т_ЗВ(min)(φ) и вносить соответствующую поправку в точке А΄, т. к. экстремальные значения для обеих кривых будут лежать на одной и той же ординате, т. е. точка А΄ должна быть перенесена в точку А, соответствующую истинному минимуму энергии маховика.

Таким образом, вместо построения кривой 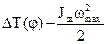на всем интервале, равном циклу, следует определить точку А по выражению:

,

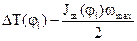где φ_i – угол, определяющий положение звена приведения, в котором кинетическая энергия будет максимальной.