Пространственная система произвольно расположенных сил.

Условие равновесия

Ранее подробно изложен процесс приведения сил к точке и доказано, что любая плоская система сил приводится к силе – главному вектору и паре, момент которой называется главным моментом, причем эквивалентные данной системе сил сила и пара действуют в той же плоскости, что и заданная система. Значит, если главный момент изобразить в виде вектора, то главный вектор и главный момент плоской системы сил всегда перпендикулярны друг другу.

Рассуждая аналогично, можно последовательно привести к точке силы пространственной системы. Но теперь главный вектор есть замыкающий вектор пространственного (а не плоского) силового многоугольника; главный момент уже нельзя получить алгебраическим сложением моментов данных сил относительно точки приведения. При приведении к точке пространственной системы сил, присоединенные пары действуют в различных плоскостях и их моменты целесообразно представлять в виде векторов и складывать геометрически. Поэтому полученные в результате приведения пространственной системы сил главный вектор (геометрическая сумма сил системы) и главный момент (геометрическая сумма моментов сил относительно точки приведения), вообще говоря, не перпендикулярны друг другу.

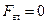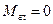Векторные равенства и выражают необходимое и достаточное условие равновесия пространственной системы произ­вольно расположенных сил.

Если главный вектор равен нулю, то его проекции на три взаим­но перпендикулярные оси также равны нулю. Если главный момент равен нулю, то равны нулю и три его составляющие на те же оси.

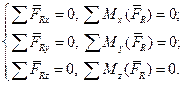
Значит, произвольная пространственная система сил статически определима лишь в том случае, когда число неизвестных не превышает шести.

Среди задач статики часто встречаются такие, в которых на тело действует пространственная система параллельных друг другу сил.

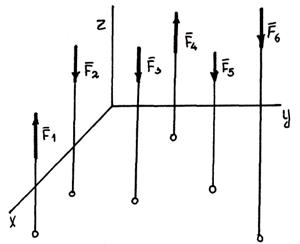
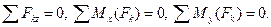
В пространственной системе параллельных сил неизвестных должно быть не больше трех, иначе задача становится статически неопределимой.