Глава 5. Пространственная система сил

5.1. Сложение пространственной системы сходящихся сил.
Условие равновесия

Система сил, линии действия которых расположены как угодно в пространстве, называется пространственной.

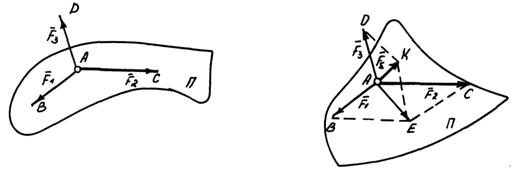
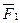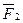Если к приложенным к точке А силам и . добавить силу 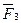, не лежащую в плоскости П действия двух первых сил, то получим простейшую (в количественном отношении) пространственную систему сходящихся сил. Определим равнодействующую этих сил. Сначала построим параллелограмм АВЕС на силах 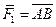и 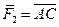. Его диагональ

.

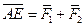Сложим АЕ с силой 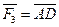и построим параллелограмм AEKD. Его диагональ

.

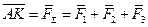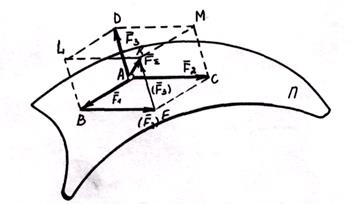
Это векторное равенство выражает правило параллелепипеда при сложении приложенных к точке трех сил, не лежащих в одной плоскости.

Параллелограмм АВЕС образует одну из граней параллелепипеда, в котором параллелограмм AEKD является диагональным сечением, а заданные силы 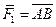, 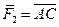и 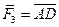ребрами одного из его трехгранных углов. Таким образом, равнодействующая пространственной системы трех сил, сходящихся в одной точке, приложена в той же точке и равна по модулю и направлению диагонали параллелепипеда, ребра которого равны и параллельны заданным силам.

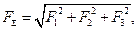
т.е. модуль равнодействующей трех сходящихся сил, расположенных в пространстве перпендикулярно друг другу, равен корню квадратному из суммы квадратов модулей этих сил.

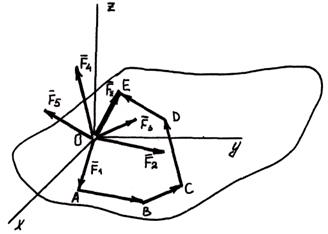
Равнодействующая любого числа сходящихся сил, расположенных в пространстве, равна замыкающей стороне многоугольника, стороны которого равны и параллельны заданным силам (правило силового многоугольника).

Аналитическое условие равновесия пространственной системы сходящихся сил выражается тремя уравнениями:

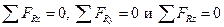
т.е. для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на каждую из трех осей координат были равны нулю.