Способы задания движения точки
Существует три способа: естественный, координатный, векторный.
Естественный способ задания движения точки. Если кроме траектории, на которой отмечено начало отсчета O, задана зависимость
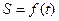
между расстоянием S и временем t, это уравнение называется законом движения точки по заданной траектории.
Пример:
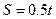
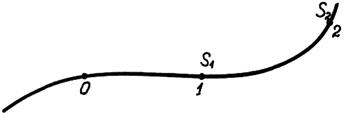
Пусть, например, задана некоторая траектория, движение точки по которой определяется уравнением 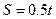
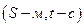 . Тогда в момент времени
. Тогда в момент времени 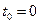
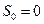 , т.е. точка находится в начале отсчета O; в момент времени
, т.е. точка находится в начале отсчета O; в момент времени 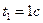 точка находится на расстоянии
точка находится на расстоянии 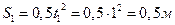 ; в момент времени
; в момент времени 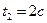 точка находится на расстоянии
точка находится на расстоянии 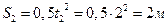 от начала отсчета O.
от начала отсчета O.
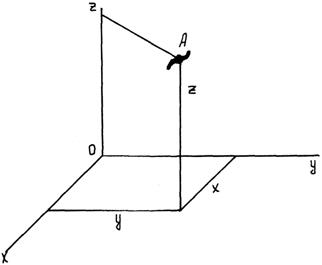
Координатный способ задания движения точки. Когда траектория точки заранее не известна, положение точки в пространстве определяется тремя координатами: абсциссой X, ординатой Yи аппликатой Z.
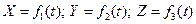 или
или 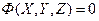 , исключив время.
, исключив время.
Эти уравнения выражают закон движения точки в прямоугольной системе координат (OXYZ).
В частном случае, если точка движется в плоскости, закон движения точки выражается двумя уравнениями: 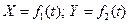 или
или 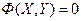 .
.
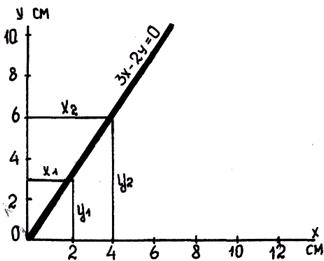
Например. Движение точки в плоской системе координат задано уравнениями 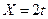 и
и 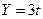 (X и Y – см, t – с). Тогда в момент времени
(X и Y – см, t – с). Тогда в момент времени 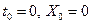 и
и 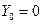 , т.е. точка находится в начале координат; в момент времени
, т.е. точка находится в начале координат; в момент времени 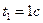 координаты точки
координаты точки 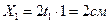 ,
, 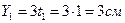 ; в момент времени
; в момент времени 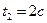 координаты точки
координаты точки 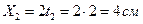 ,
, 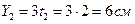 и т.д.
и т.д.
Зная закон движения точки в прямоугольной системе координат, можно определить уравнение траектории точки.
Например, исключив время t из заданных выше уравнений 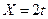 и
и 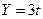 , получим уравнение траектории
, получим уравнение траектории 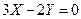 . Как видим, в этом случае точка движется по прямой, проходящей через начало координат.
. Как видим, в этом случае точка движется по прямой, проходящей через начало координат.
6.3. Определение скорости точки при естественном способе
задания ее движения
Пусть движение точки А по заданной траектории происходит согласно уравнению 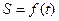 , требуется определить скорость точки в момент времени t.
, требуется определить скорость точки в момент времени t.
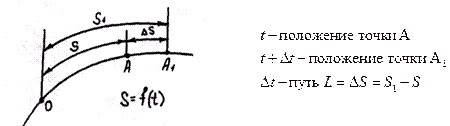
За промежуток времени 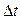 точка прошла путь
точка прошла путь 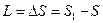 , значение средней скорости на этом пути
, значение средней скорости на этом пути
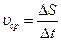 ,
,
но оно отличается от значения скорости в момент времени t. Скорость в заданный момент t
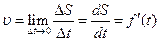 ,
,
т.е. значение скорости точки, движение которой задано естественным способом, в любой момент времени равно первой производной от расстояния (дуговой координаты) по времени.
Направление скорости, как отмечалось выше, известно заранее.
6.4. Определение ускорения точки при естественном способе
задания ее движения
Вектор 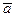 – ускорение точки в данный момент – есть геометрическая сумма касательного
– ускорение точки в данный момент – есть геометрическая сумма касательного 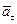 и нормального
и нормального 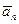 ускорений:
ускорений:
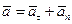
Вектор 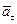 в любой момент времени направлен по касательной, поэтому вектор
в любой момент времени направлен по касательной, поэтому вектор 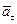 называется касательным, илитангенциальным ускорением. Модуль касательного ускорения
называется касательным, илитангенциальным ускорением. Модуль касательного ускорения
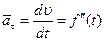 ,
,
равный производной от скорости в данный момент по времени или, иначе, второй производной от расстояния по времени, характеризует быстроту изменения значения скорости.
Доказано, что вектор 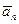 в любой момент времени перпендикулярен касательной, поэтому он называется нормальным ускорением.
в любой момент времени перпендикулярен касательной, поэтому он называется нормальным ускорением.
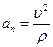
Значит, модуль нормального ускорения пропорционален второй степени модуля скорости в данный момент, обратно пропорционален радиусу кривизны траектории в данной точке и характеризует быстроту изменения направления скорости.

Модуль ускорения
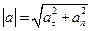 ,
,
а направление a (угол 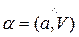 ) находим с помощью тригонометрических функций по одной из следующих формул:
) находим с помощью тригонометрических функций по одной из следующих формул:
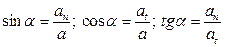 .
.
Если векторы 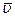 и
и 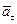 направлены в одну и ту же сторону, то движение точки называется ускоренным. При этом значения
направлены в одну и ту же сторону, то движение точки называется ускоренным. При этом значения 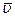 и
и 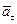 имеют одинаковые знаки (
имеют одинаковые знаки ( 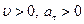 или
или 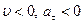 ). Если же векторы
). Если же векторы 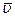 и
и 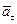 направлены в противоположные стороны, то движение точки называется замедленным. В этом случае знаки
направлены в противоположные стороны, то движение точки называется замедленным. В этом случае знаки 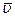 и
и 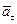 разные (
разные ( 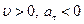 или
или 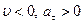 ).
).
Дата добавления: 2021-12-14; просмотров: 603;











