Момент силы относительно оси
Обозначив момент силы 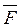 относительно осей
относительно осей 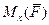 ,
, 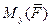 и
и 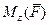 , можем записать:
, можем записать:
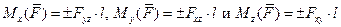
где 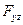 ,
, 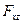 и
и 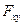 модули проекций сил на плоскости, перпендикулярные той оси, относительно которой определяется момент; l – плечи, равные длинам
модули проекций сил на плоскости, перпендикулярные той оси, относительно которой определяется момент; l – плечи, равные длинам
перпендикуляров от точки пересечения оси с плоскостью до проекции или ее продолжения; знак «плюс» или «минус» ставится в зависимости от того, в какую сторону поворачивается плечо l вектором проекции, если смотреть на плоскость проекции со стороны положительного направления оси; при стремлении вектора проекции повернуть плечо против хода часовой стрелки момент условимся считать положительным, и наоборот.
Следовательно, моментом силы относительно оси называется алгебраическая (скалярная) величина, равная моменту проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
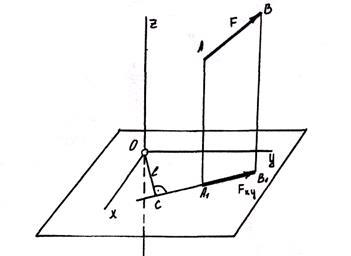
Предыдущий рисунок иллюстрирует последовательность определения момента силы 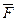 относительно оси Z. Если задана сила и выбрана (или задана) ось, то: а) перпендикулярно оси выбирают плоскость (плоскость ХОУ); б) силу F проецируют на эту плоскость и определяют модуль
относительно оси Z. Если задана сила и выбрана (или задана) ось, то: а) перпендикулярно оси выбирают плоскость (плоскость ХОУ); б) силу F проецируют на эту плоскость и определяют модуль 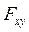 этой проекции; в) из точки 0 пересечения оси с плоскостью опускают перпендикуляр ОС к проекции
этой проекции; в) из точки 0 пересечения оси с плоскостью опускают перпендикуляр ОС к проекции 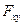 и определяют плечо l = ОС; г) глядя на плоскость ХОУ со стороны положительного направления оси Z (т.е. в данном случае сверху), видим, что ОС поворачивается вектором
и определяют плечо l = ОС; г) глядя на плоскость ХОУ со стороны положительного направления оси Z (т.е. в данном случае сверху), видим, что ОС поворачивается вектором 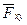 против хода стрелки часов, значит
против хода стрелки часов, значит
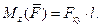
Момент силы относительно оси равен нулю, если сила и ось лежат в одной плоскости: а) сила 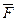 пересекает ось (в этом случае l = 0);
пересекает ось (в этом случае l = 0);
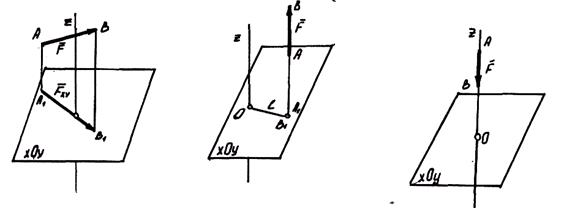
б) сила 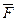 параллельна оси (
параллельна оси ( 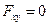 );
);
в) сила 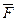 действует вдоль оси (l=0 и
действует вдоль оси (l=0 и 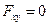 ).
).
Дата добавления: 2021-12-14; просмотров: 503;











