Типові завдання оптимізації

Простим окремим випадком класичних оптимізаційних завдань є завдання на пошук екстремумів нелінійної цільової функції. Подібне завдання розглядалося у п.1. Якщо, для двох пар змінних стану й управління цільова функція має вигляд

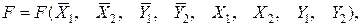
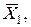
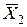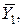
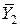де й - координати оптимуму, те переходячи звичайним чином від подання цільової функції у вигляді 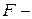форми до 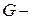форми, можна вивести умови, при яких буде забезпечуватися її максимум (або мінімум). Причому вони обов'язково є, оскільки екстремальні крапки у функції існують.

Умовою максимуму є:

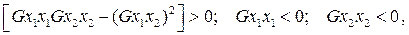
де 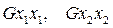— друга частинна похідна відповідно від 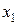і по 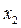; 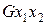— змішана частинна похідна.

Для мінімуму умова 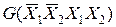відповідно має вигляд

.

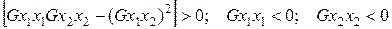Часто в теорії оптимізації зустрічаються завдання на оптимізацію нелінійної цільової функції з нелінійними обмеженнями. Для знаходження оптимальних значень, за якими проводиться оптимізація, застосовується метод множників Лагранжа.

Аналіз змісту завдання даного типу приводить до наступних співвідношень: цільова функція може бути подана як сума її деякого приватного виду , що відповідає мінімальному значенню, отриманому в процесі оптимізації при відсутності обмежень, і функції обмежень , узятої з деяким множником :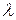

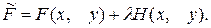
У випадку, коли задано т обмежень, цільова функція має вигляд:

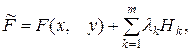
а умови оптимуму становлять систему наступних рівнянь:

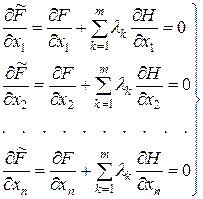
Більшу групу оптимізаційних завдань становлять завдання лінійного програмування. Лінійні моделі у відсутності обмежень не мають кінцевих значень змінних, визначальний мінімум або максимум цільових функцій. Сукупність деякого числа лінійних обмежень визначає в 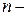мірному виробництві відповідний опуклий багатогранник, вершинами якого є координати 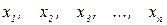. Будь-яке вираження виду 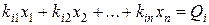визначає гіперплощина х-мерного простору. При т числі обмежень утвориться т гіперплощин, причому перетинання будь-яких двох з них дає в перетині деякий багатогранник (рис. 10).

Рисунок 10 - Лінійне програмування й симплекс-метод

Рішення завдань подібного типу проводиться за допомогою так званого симплексного методу, сутність якого полягає у знаходженні координат однієї з вершин і наступному спрямованому русі по ребрах багатогранника, отриманого у результаті перетинання х-мерного опуклого багатогранника з гіперплощиною виду

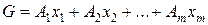. (41)

Рух повинен проводиться тільки або убік зменшення значення цільової функції при її мінімізації, або убік збільшення при пошуку максимуму.

Серед інших класичних завдань оптимізації велике місце посідають завдання, розв'язувані із застосуванням методів варіаційного обчислення й динамічного програмування.