Цільові функції оптимізації

При рішенні завдання оптимізації важливо визначити основні принципи завдання цільових функцій. Серед них основними є наступні.

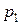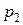1 Принцип однозначності, який полягає в тому, що в рамках одного завдання повинна оптимізуватися одна й тільки одна цільова функція. Для цього необхідно, щоб набір окремих складових і загальної цільової функції 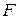набув виду:

,

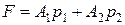де 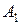й 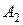— вагомі коефіцієнти.

Якщо одна функція 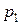повинна максимізуватися, а інша р2 мінімізуватися, то доцільно одну з них замінити на зворотну 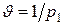, щоб при оптимізації шукати загальний максимум.

2 Принцип відповідності, який полягає в такому виборі, щоб оптимізація цільової функції забезпечувала найкращі результати, тобто впливала істотно на результат.

3 Принцип модифікації, який означає, що цільова функція має бути виражена через змінні, що піддаються цілеспрямованому впливу й зміні.

4 Принцип відповідної форми, відповідно до якого функції, які мають розриви, локальні екстремуми й неоднозначності, є небажаними для вибору їх як цільові функції. Найпоширенішими видами цільових функцій є:

ЦФ економічної ефективності (прибутку):

,

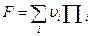де 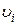- коефіцієнт ефективності 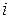-го компонента процесу (системи); 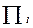- -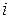й позитивний ефект процесу; 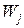- вартість 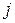-го ресурсу; 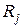- витрата 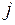-го ресурсу.

ЦФ вартості:

,

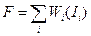де 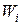- вартість одержання результату 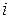-го виходу; для ІМ 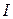- кількість інформації з 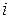-му виходу.

ЦФ якості:

,

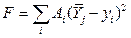де 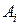- позитивні вагові коефіцієнти; 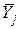- настановні значення змінні стани.

При оптимізації більшу роль грають обмеження, серед яких розрізняють наступні види:

- тверді обмеження на змінні управління, загальна форма яких може бути виражена нерівностями: ;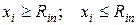

- нежорсткі обмеження на змінні управління, що враховуються непрямим чином через так звану функцію штрафу: 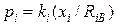, де 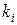, М - позитивні числа; 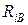— величина обмеження; можливий та інший вид функції штрафу: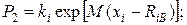

- обмеження на змінні стани й змінні управління, виражені як функції змінних управління (умови обмежень):

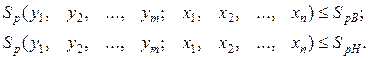
Модель дозволяє звести ці умови до такого виду, що обмеження будуть задані тільки у вигляді функцій змінних управління:

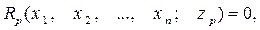
де 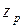- допоміжна змінна.

Співвідношення, розглянуті вище й використовувані при рішенні оптимізаційних завдань, показують основний зміст і призначення моделей досліджуваних процесів. Вони також дають можливість правильно ідентифікувати різні інформаційні параметри й величини; здійснювати постановку завдань моделювання й установлення зв'язків між різними змінними; вибрати й обґрунтувати критерії оптимізації, визначити цільові функції; задати обмеження; здійснити постановку оптимізаційного завдання й попередньо оцінити адекватність розроблювальної моделі.