Оброблення даних імітації

Основними методами оброблення даних імітаційного експерименту є:

- регресійний аналіз (РА);

- дисперсійний аналіз;

- статистична обробка.

Розглянемо деякі теоретичні положення, що дозволяють обробити дані експериментів і правильно інтерпретувати отримані результати моделювання. Основою будь-якого імітаційного експерименту на ЕОМ служить вихідна формалізована модель імітованої системи.

У найбільш загальному виді формалізована модель для більшості систем ґрунтується на концепціях кінцевих автоматів:

,

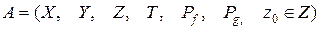де X - кінцева безліч вхідних сигналів, кожний елемент якого вектор постійної розмірності; Z - кінцева непуста безліч станів, обумовлених за допомогою вектора станів; Y - кінцева безліч вихідних сигналів; Т - частково впорядковане (за відношенням 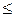) безліч моментів часу 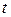; 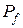- таблиця умовних функціоналів переходів абстрактного автомата, отримана відповідно до опису модельованого процесу (причому перехід автомата з одного стану до іншого відбувається практично миттєво); - таблиця умовних функціоналів виходів, за допомогою якої описується процес формування вихідних сигналів у ті моменти часу, коли внаслідок надходження вхідного сигналу автомат переходить до нового стану.

Похибка формалізованої моделі у загальному випадку може виявитися досить значною. Але коли вона невідома, то можна йти від найпростіших моделей убік ускладнення їх у міру необхідності. Критерієм можливості застосування деякого варіанта формалізованої моделі служить її точність і адекватність. Оцінка адекватності, аналіз і обробка результатів моделювання проводяться відповідно до обраної методики з безлічі можливих варіантів. Окремі методики, призначені для зазначеної мети, у деталях можуть відрізнятися один від одного, але в головних рисах вони повинні відповідати наведеній загальній схемі моделювання.

Регресійний аналіз. Розглянемо на прикладі побудови формалізованої лінійної моделі з наступним переходом до більше складних моделей можливий варіант методики обробки результатів імітаційного експерименту. Нехай, за припущенням, модельованій системі відповідає лінійна модель, що доцільно прийняти за вихідну на першому етапі моделювання:

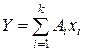, (25)

де 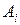- деякі параметри модельованої системи; { 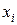} - фактори; - реакції.

Якби була можливість проводити усі експерименти, то, змінюючи фактор 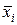у заданому діапазоні значень і спостерігаючи реакцію 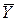, можна було б оцінити досить точно параметр 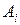. Однак на практиці кількість експериментальних значень обмежено, тому їх потрібно логічно обґрунтувати, а потім інтерпретувати побудовану модель

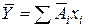, (26)

де 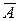й 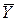позначають оцінки величин 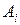і відповідно.

Розглянемо, як варто встановлювати найбільш відповідні значення шуканих параметрів, щоб модель була по можливості більше точною. Для лінійних моделей маємо:

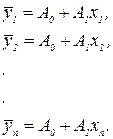
Помилки, що являють собою розбіжність між ідеалізованими значеннями й експериментальними даними, відповідно рівні:

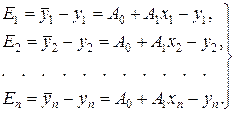
Функція (критерій) результуючої середньоквадратичної помилки визначається так:

(27)

Умова мінімуму (27):

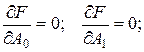
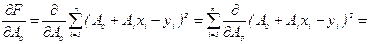
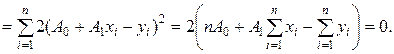
Аналогічним образом знайдемо

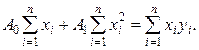
Одержимо, таким чином, систему рівнянь, що випливає:

.

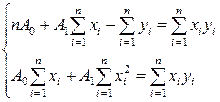Її рішення дає наступний результат:

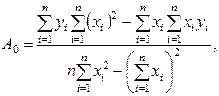(28)

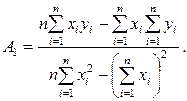(29)

За міру помилки моделі беруть стандартне відхилення, тобто

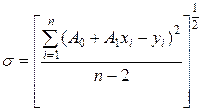. (30)

Коефіцієнти 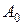, 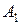щонайкраще задовольняють умовам мінімуму 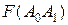помилки, якщо вони перебувають із 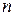систем лінійних алгебраїчних рівнянь із двома невідомими ( 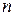— кількість даних експерименту) і зводяться до деяких сталих значень , , 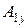що не залежать від .

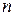Кромі лінійних моделей можуть зустрітися моделі більше високих порядків [5]. Наприклад:

- поліноміальні моделі другого порядку:

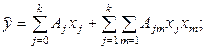(31)

- мультиплікативна регресійна модель:

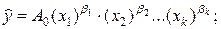
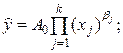(32)

- експонентна модель:

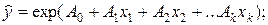(33)

- оборотна модель:

(34)

Шляхом відповідних математичних перетворень (апроксимації й т.д.) ці моделі спочатку зводять до лінійних, а потім досліджують.

Дисперсійний аналіз. Для визначення моделі, якій відповідають одержувані під час експерименту дані, досить докладну інформацію дає метод дисперсійного фактора аналізу (ТАК).

Загалом ТАК - це метод, що дозволяє досліджувати питання впливу окремих факторів на реакцію, а також їхній можливий взаємовплив.

У процесі дисперсійного аналізу вибирають яких-небудь два фактори із загальної їхньої безлічі , 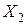. Щоб спростити індексування, уведемо нові позначення М і N. Фізичною сутністю, що відповідає цим факторам, у випадку моделювання інформаційних мереж, можуть бути: М — число джерел повідомлень, N - обсяг переданих повідомлень.

Метод дисперсійного факторного аналізу ґрунтується на припущенні про незалежність факторів, нормальності розподілу значень факторів і реакції, а також на збіжності значень дисперсії реакцій.

З метою з'ясування впливу факторів 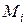, 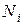розглядають 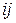варіанти їхніх обраних значень, для кожного з яких визначається безліч значень реакцій 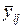( 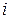- номер варіантів значень фактора М, 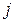- фактора 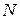). Для цього становлять таблицю наступного виду (табл. 4).

Під у може розумітися інтегрально-пропускна здатність мережі, тоді елементи, зазначені в таблиці, означають наступне: 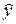- середнє значення інтегральної пропускної здатності ІМ при 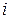-м варіанті кількості джерел при 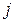- варіанті середнього обсягу переданих повідомлень, , - середня за всіма варіантами обсягу повідомлень і за 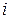-м варіантом кількості джерел пропускна здатність ІМ; ; - середня за всіма варіантами числа джерела при ; 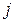-м варіанті обсягу вхідних повідомлень.

Аналізуючи значення різних величин, одержуваних у результаті підрахунку окремих різностей виду 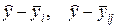й т.п., можна оцінити вплив факторів М і N на значення реакції. Крім того, у принципі може бути визначений і взаємовплив факторів один на одного в моделі, а отже, з певною ймовірністю й у самій системі.

При відсутності взаємодії факторів у моделі середнє за клітинкою табл. 4 може бути виражене через інші середні й деякі допоміжні величини. Такими величинами є так звані ефекти рядків і стовпців.

Таблиця 4 – Вплив факторів 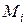і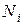

Можливі варіанти числа джерел повідомлення	Обсяги переданих повідомлень

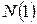
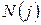
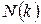
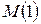
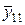
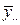
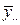
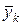
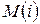
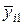
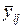
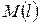
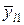
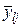
Головним ефектом рядка (стовпця) уважається, зокрема, відхилення загального середнього за рядком ,- (за стовпцем 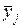) від середнього за всією таблицею:

.

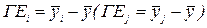Якщо взаємодія відсутня, то виконується наступне співвідношення:

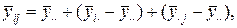(35)

у противному випадку фактори М и N не адитивні, тобто не можуть розглядатися окремо.

Розглянуті принципи оцінки дії двох факторів 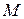і 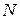на реакцію й облік їхнього взаємовпливу можуть бути узагальнені й на випадок більшої кількості факторів, однак при цьому природно ускладнюються обчислення їхніх ефектів. Крім того, може ускладнитися сама модель і втратити свою точність і адекватність.