Плоская система сил

Напомним, что плоской системой сил, приложенных к твердому телу, называют такую систему сил, линии действия которых лежат в одной плоскости, например, в плоскости xoy прямоугольной системы координат.

Для плоской системы сил главный вектор 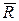лежит в плоскости действия сил. Все присоединенные пары сил тоже лежат в этой плоскости. Следовательно, векторные моменты этих пар перпендикулярны плоскости действия сил и взаимно параллельны.

Приведем формулы для вычисления главного вектора и главного момента для плоской системы. Согласно (5.8) и (5.9) для вычисления главного вектора имеем

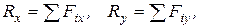(5.13)

.

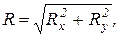
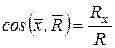Главный момент плоской системы перпендикулярен плоскости действия главного вектора. Если ось z перпендикулярна плоскости xoy, то координаты главного момента относительно центра приведения О, согласно (5.2) равны

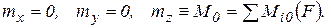(5.14)

Здесь M₀ – z- я компонента алгебраического главного момента.

Для плоской системы сил вместо векторного главного момента 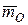используют понятие алгебраического главного момента M₀ .

Сформулируем основную теорему статики для плоской системы сил, действующих на твердое тело:

любая произвольная плоская система сил, приложенных к твердому телу, эквивалентна системе, состоящей из одной силы приложенной в какой-либо точке О тела и раной главному вектору 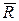, и одной пары, момент которой равен алгебраическому главному моменту M₀.

5.6. Теорема Вариньона для системы сходящихся сил (теорема о моменте равнодействующей)

Теорема. Момент относительно центра О равнодействующей 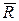системы сходящихся сил 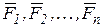, расположенных в одной плоскости, равен алгебраической сумме моментов сил системы относительно того же центра:

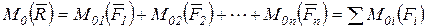. (5.15)

Здесь .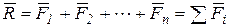

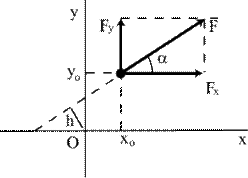
	Например, момент силы m0(F) (рис.5.8) определяется относительно начала координат по формуле m0(F)= -F·h, где h неизвестно. Воспользуемся теоремой Вариньона: M0(F)= M0(Fx)+ M0(Fy)=x0Fy-y0Fx.
Рис.5.8