Приведение силы к заданному центру

Теорема. Силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векторный момент которой равен векторному моменту переносимой силы относительно новой точки приложения силы. Пусть имеем силу 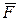, приложенную к твердому телу в точке А в плоскости П (рис.5.6а). Покажем, что силу можно переносить на другую, параллельную линию действия. Но этот перенос следует компенсировать добавлением соответствующей пары сил.	а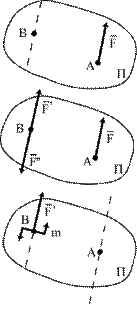
б
в
Рис.5.6

В соответствии с аксиомой 2, приложим в точке В, выбранной за центр приведения, равновесную систему сил (систему двух равных по модулю, но противоположных по направлению сил) 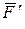и 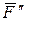, параллельных заданной силе 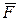. Пусть модули этих сил равны между собой: F=F^'=F^''.

Тогда система сил 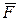и 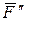составят пару сил, которую называют присоединенной парой сил (рис.5.6б), модуль момента которой m=Fd (d- минимальное расстояние между линиями действия сил).

Итак, вместо силы 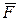, приложенной в точке А, получена сила 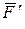, равная ей по модулю и направлению, но приложенная в точке В, и присоединенная пара сил, векторный момент которой

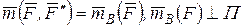. (5.5)