Момент силы относительно центра и оси
Моментом силы (моменты пар сил имеют противоположные 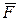 относительно центра О называется вектор
относительно центра О называется вектор 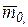 равный векторному произведению радиуса вектора
равный векторному произведению радиуса вектора 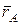 , соединяющего центр О с точкой приложения силы А, на саму силу
, соединяющего центр О с точкой приложения силы А, на саму силу 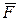 .
.
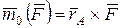 . (5.1)
Вычислим . (5.1)
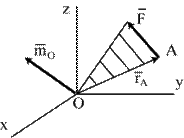
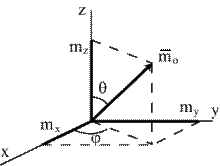
Вычислим 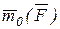 аналитически (рис.5.1). Пусть заданы проекции радиус-вектора аналитически (рис.5.1). Пусть заданы проекции радиус-вектора 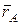 (xA, yA, zx) и проекции силы (xA, yA, zx) и проекции силы 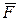 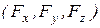 . .
| 
|
| Рис.5.1 |
Тогда, раскрывая векторное произведение в (5.1), по известной формуле векторной алгебры имеем:
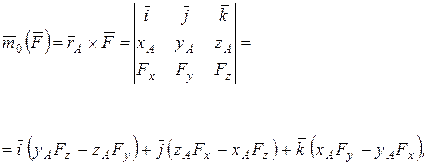 (5.2)
(5.2)
где 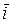 ,
, 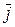 ,
, 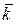 - единичные орты.
- единичные орты.
Поскольку 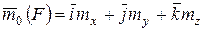 , то
, то 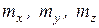 - координаты момента
- координаты момента 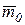 на оси x, y, z, которые соответственно равны:
на оси x, y, z, которые соответственно равны:
mx=yAFz- zAFy, my=zAFx- xAFz, mz=xAFy- yAFx
Моментом силы 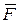 относительно оси будем называть проекцию на эту ось вектора момента
относительно оси будем называть проекцию на эту ось вектора момента 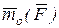 , т. е.
, т. е. 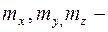 моменты силы относительно осей x, y, z соответственно. С помощью формул (5.2), момент силы относительно оси можно вычислить, зная проекции силы и координаты точки ее приложения.
моменты силы относительно осей x, y, z соответственно. С помощью формул (5.2), момент силы относительно оси можно вычислить, зная проекции силы и координаты точки ее приложения.
| направляющим косинусам:
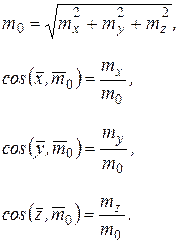 (5.2а) (5.2а)
|
| Рис.5.2 | На практике удобно пользоваться следующими |
Зная моменты силы относительно осей mx, my, mz , можно определить модуль момента силы 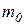 относительно центра (рис.5.2) и его направление по правилами для определения моментов
относительно центра (рис.5.2) и его направление по правилами для определения моментов 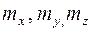 (рис.5.3).
(рис.5.3).
· Если сила параллельна оси, то ее момент относительно этой оси равен нулю (рис.5.3а).
| а | 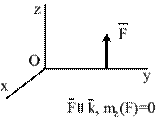
| б | 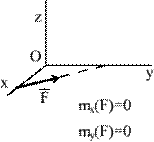
| в | 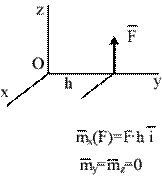
|
| Рис.5.3 |
· Если линия действия силы пересекает оси, то ее моменты относительно этих осей также равны нулю (рис.5.3б).
· Если сила перпендикулярна к оси, например к оси y (рис.5.3в) и кратчайшее расстояние между линией действия силы и осью, например осью x, равно h, то момент силы относительно оси x равен произведению модуля силы на расстояние между линией действия силы и осью.
| а | 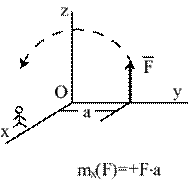
| б | 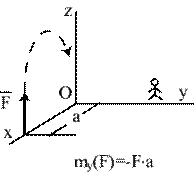
|
| Рис.5.4 |
Если сила старается развернуть твердое тело вокруг оси против хода часовой стрелки относительно наблюдателя, стоящего на этой оси, то момент силы относительно этой оси положительный (рис.5.4а); если по ходу часовой стрелки, - отрицательный (рис.5.4б).
Дата добавления: 2019-12-09; просмотров: 779;











