Кривые второго порядка
Кривыми второго порядка называются линии, уравнения которых могут быть записаны в виде:
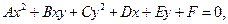
где 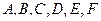 - действительный числа, причем хотя бы один из коэффициентов
- действительный числа, причем хотя бы один из коэффициентов 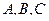 не равен нулю. Кривые второго порядка – это окружность, эллипс, гипербола, парабола.
не равен нулю. Кривые второго порядка – это окружность, эллипс, гипербола, парабола.
1. Окружность– множество точек плоскости, равноудаленных от данной точки - центра.
Символически: 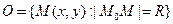 , где
, где 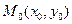 - центр,
- центр, 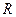 - радиус
- радиус 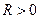
Уравнение: 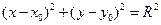
Пример: Написать уравнение окружности радиуса 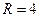 с центром в точке
с центром в точке 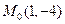
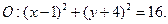
2. Эллипс – множество точек плоскости, сумма расстояний для любых из которых до двух заданных точек 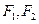 (фокусов) есть величина постоянная.
(фокусов) есть величина постоянная.
Символически: 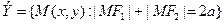 , где
, где 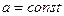 ,
, 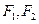 - заданные "фокусы".
- заданные "фокусы".
Уравнение: Примем координаты фокусов 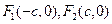 . Тогда для произвольной точки эллипса
. Тогда для произвольной точки эллипса 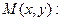
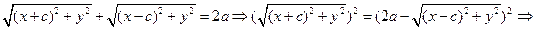
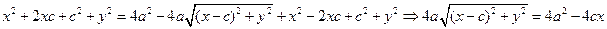
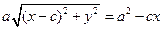 (1)
(1)
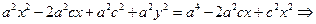
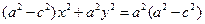 (2)
(2)
Так как 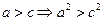 . Обозначим
. Обозначим 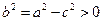 Подставляя в равенство (??0), получим
Подставляя в равенство (??0), получим
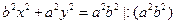
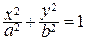 – каноническое уравнение эллипса.
– каноническое уравнение эллипса.
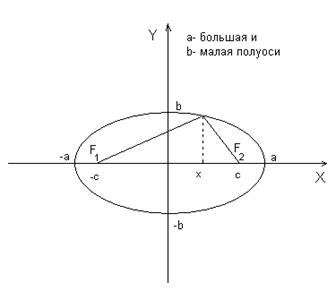
Эксцентриситет эллипса: 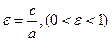 - характеризует степень сжатия эллипса. Действительно:
- характеризует степень сжатия эллипса. Действительно:
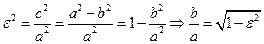
Чем больше e, тем меньше 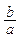 т.е. эллипс "вытягивается" вдоль оси
т.е. эллипс "вытягивается" вдоль оси  . При
. При 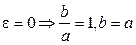 - приходим к уравнению окружности.
- приходим к уравнению окружности.
Пример. Найти параметры a, b, c и эксцентриситет эллипса, заданного уравнением: 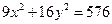 . Приведем уравнение к каноническому виду, деля обе части на 576
. Приведем уравнение к каноническому виду, деля обе части на 576
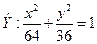
откуда: 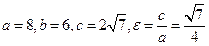
3. Гипербола - множество точек плоскости, разность расстояний для любой из которых до двух заданных точек  (фокусов) есть величина постоянная.
(фокусов) есть величина постоянная.
Символически: 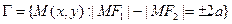 , где
, где 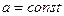 ,
, 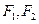 - заданные "фокусы".
- заданные "фокусы".
Уравнение: Принимая координаты фокусов 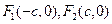 и проведя преобразования, аналогичные выводу уравнения эллипса, придем к каноническому уравнению гиперболы:
и проведя преобразования, аналогичные выводу уравнения эллипса, придем к каноническому уравнению гиперболы:
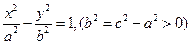
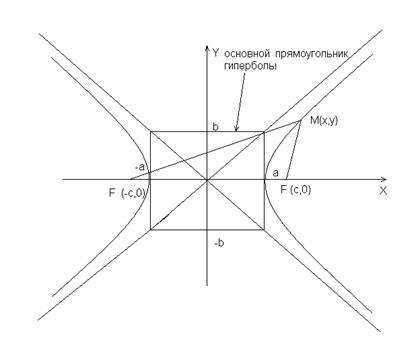
Асимптоты гиперболы: 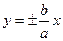 , эксцентриситет:
, эксцентриситет: 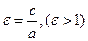
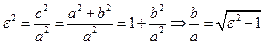
Если 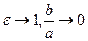 основной прямоугольник "вытягивается" вдоль оси
основной прямоугольник "вытягивается" вдоль оси  . В случае
. В случае 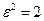 , т.е.
, т.е. 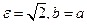 - гипербола "равнобочная".
- гипербола "равнобочная".
Пример. Найти полуоси 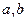 фокальное расстояние
фокальное расстояние 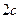 , асимптоты и эксцентриситет гиперболы
, асимптоты и эксцентриситет гиперболы 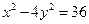 .
.
Деля обе части на 36, получим
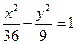
Откуда, 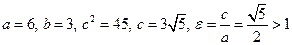 . Асимптоты
. Асимптоты 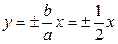
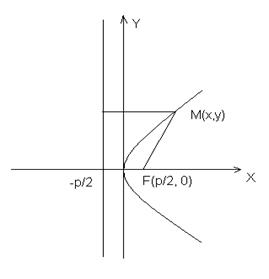
4. Парабола – множество точек плоскости, равноудаленных от данной точки  - "фокуса" и данной прямой
- "фокуса" и данной прямой 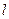 - "директрисы" Символически:
- "директрисы" Символически: 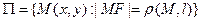 , где
, где 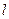 -"директриса",
-"директриса", 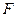 - заданный "фокус".
- заданный "фокус".
Уравнение: Примем уравнение директрисы 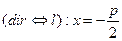 ; координаты фокуса
; координаты фокуса 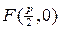 . Тогда уравнение параболы:
. Тогда уравнение параболы:
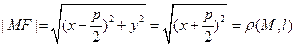
После преобразования получим: 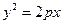 -каноническое уравнение параболы (p– параметр параболы)
-каноническое уравнение параболы (p– параметр параболы)
Замечание. Если директрису расположить параллельно оси OX, а фокус - на оси OY, то можно получить каноническое уравнение параболы в виде 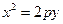
Пример. Составить каноническое уравнение параболы, проходящей через точку 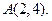 a) Если принять уравнение параболы
a) Если принять уравнение параболы 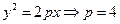 ,
, 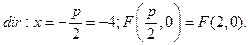
б) Можно принять уравнение параболы
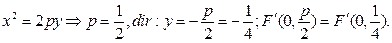
Дата добавления: 2016-06-05; просмотров: 2148;











