Обратная задача кинематики

В этом разделе рассматривается обратная задача кинематики шестизвенного манипулятора. Необходимо по заданной матрице ⁰T₆ положения и ориентации схвата шестизвенного манипулятора и известным параметрам его звеньев и сочленений определить присоединенные параметры 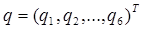манипулятора, обеспечивающие заданное положение схвата.

Для того, чтобы решение обратной задачи кинематики было получено в явном виде, необходимо, чтобы конструкция робота удовлетворяла одному из двух условий:

1. Оси трех смежных сочленений пересекаются в одной точке.

2. Оси трех смежных сочленений параллельны между собой.

Из равенства (4-2) следует вид матрицы манипулятора T:

T₆= 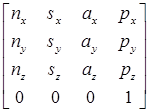=⁰A₁ ¹A₂ ²A₃ ³A₄ ⁴A₅ ⁵A₆. (6-7)

Из равенства (4-7) видно, что матрица T является функцией синусов и косинусов углов 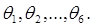Приравнивая элементы матриц в левой и правой частях матричного уравнения (4-7), получаем, например, для манипулятора Пума двенадцать уравнений (4-3) – (4-6) относительно шести неизвестных (присоединенных углов). Поскольку число уравнений превышает число переменных, можно сразу сделать вывод о том, что решение обратной задачи кинематики для манипулятора Пума не единственно. Мы рассмотрим два метода решения обратной задачи кинематики: метод обратных преобразований в эйлеровых координатах и геометрический подход, выгодно отличающийся наглядностью.