Тождественные преобразования и применение таблиц 1 и 2.

Пример 1. Найти оригинал для изображения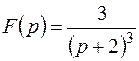

Решение.

Преобразуем 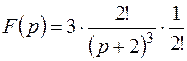на основании теоремы смещения: 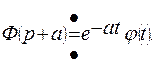имеем

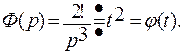
Тогда,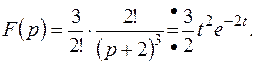

Пример 2. Найти оригинал для изображения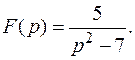

Решение.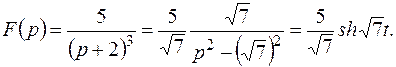

Пример 3. Найти оригинал для изображения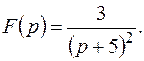

Решение.

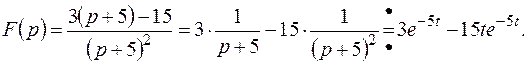
Пример 4. Найти оригинал для изображения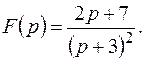

Решение.

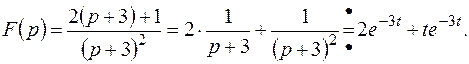
Пример 5. Найти оригинал для изображения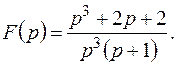

Решение.

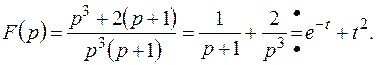
Пример 6. Найти оригинал для изображения

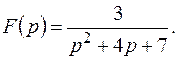
Решение.

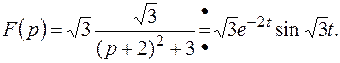
Пример 7. Найти оригинал для изображения

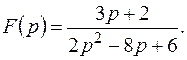
Решение.

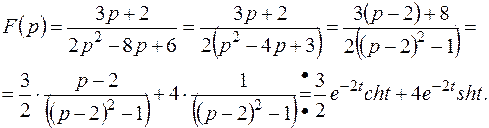
Пример 8. Найти оригинал для изображения

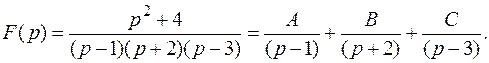
Отсюда следует равенство

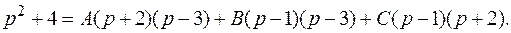
Для нахождения 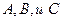используем метод частных значений.

При:

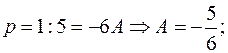
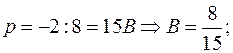
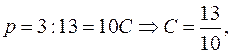поэтому

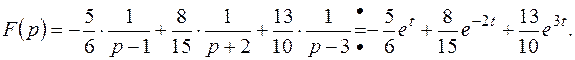
Пример 9. Найти оригинал для изображения

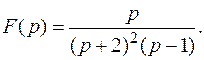
Решение.

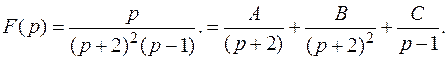
Отсюда следует равенство:

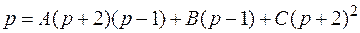
При:

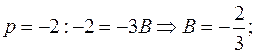
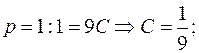
Приравнивая коэффициенты при 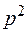получим:

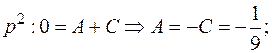
Тогда

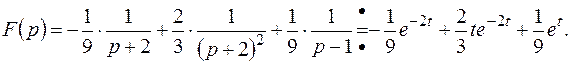
Пример 10. Найти оригинал для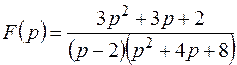

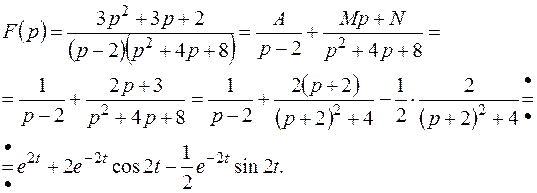
Пример 11. .Найти оригинал для .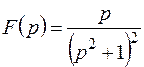

Решение.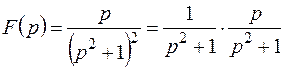

Так как 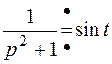, , 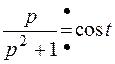то по теореме Бореля

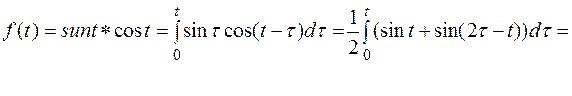
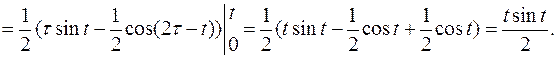
Пример 12. Найти оригинал для изображения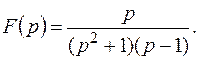

Решение.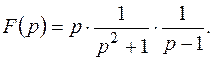

Так как 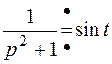, , 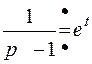то используя интеграл Дюамеля, получим

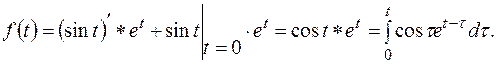
Вычислим:

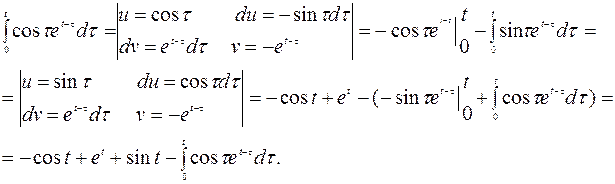Отсюда:

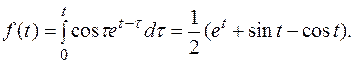
Этот пример можно решить иначе.

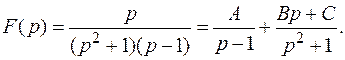
Отсюда следует равенство:

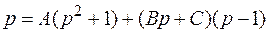
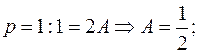
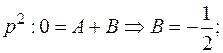
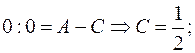
Тогда: