Вычисление оригиналов с помощью вычетов.
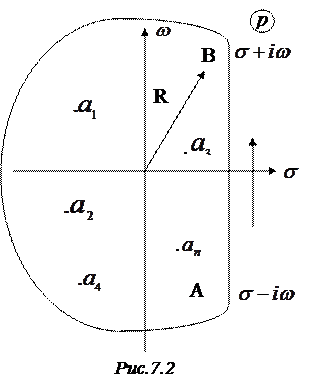 Будем предполагать, что
Будем предполагать, что 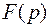 функция аналитическая во всей комплексной плоскости p, за исключением, конечного числа особых точек
функция аналитическая во всей комплексной плоскости p, за исключением, конечного числа особых точек 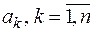 и удовлетворяет условию
и удовлетворяет условию 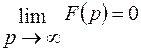 , а также предполагается аналитичность
, а также предполагается аналитичность 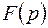 в бесконечно удаленной точке. Для вычисления
в бесконечно удаленной точке. Для вычисления 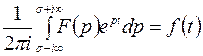 поступим следующим образом. Возьмем контур Г, состоящий из дуги BA окружности
поступим следующим образом. Возьмем контур Г, состоящий из дуги BA окружности 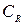 и отрезка AB (рис.7.2).
и отрезка AB (рис.7.2).
Радиус R выберем таким большим, чтобы все особые точки попали в область, ограниченную контуром Г, тогда:
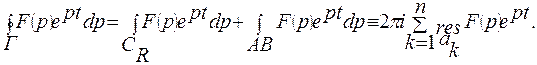
Особый интерес представляет собой случай, когда 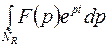 при
при 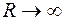 исчезает.
исчезает.
Лемма Жордана.
Если 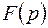 на
на 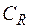 стремится к нулю при
стремится к нулю при 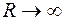 равномерно относительно
равномерно относительно 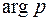 , то для любого
, то для любого 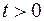
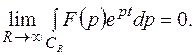
Итак, при 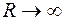 и выполнении условия леммы Жордана имеем
и выполнении условия леммы Жордана имеем
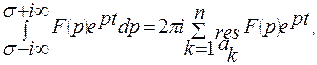 откуда по формуле обращения получим:
откуда по формуле обращения получим:
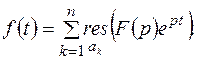 (7.2)
(7.2)
Формулу (7.2) называют второй теоремой разложения. Она позволяет в самом общем случае найти оригинал по его изображению. Но очень часто F(p) представляет собой дробно-рациональную функцию, что позволяет упростить вычисления оригиналов.
Пусть
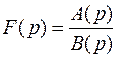 ,
,
где А(р) и В(р)- многочлены степени m и n, соответственно, причем m<n.
1.Случай простых полюсов.
Применяя формулу для нахождения вычета относительно простого полюса от функции представимой в виде частного двух выражений, получим:
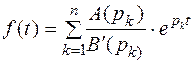 (7.3)
(7.3)
Здесь 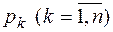 простые полюса.
простые полюса.
2.Случай кратных полюсов.
Пусть 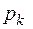 - полюсы кратности
- полюсы кратности 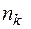 и таких различных полюсов будет l, тогда
и таких различных полюсов будет l, тогда
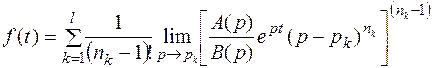 (7.4)
(7.4)
3.Случай комплексно – сопряженных полюсов:
Пусть 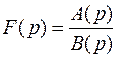 имеет простые комплексно – сопряженные корни
имеет простые комплексно – сопряженные корни 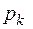 и
и 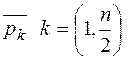 . Мы знаем, что комплексно- сопряженные корни появляются парами, а т.к. мы рассматриваем полиномы А(р) и В(р) с действительными коэффициентами, то после подстановки корней получим сопряженные выражения т.е.
. Мы знаем, что комплексно- сопряженные корни появляются парами, а т.к. мы рассматриваем полиномы А(р) и В(р) с действительными коэффициентами, то после подстановки корней получим сопряженные выражения т.е.
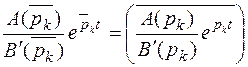
Теперь после подстановки корней в (7.3) мы получим, что выражение от пары комплексно- сопряженных корней дают:
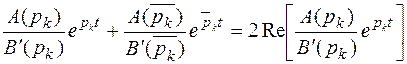 .
.
В результате получим формулу для данного случая
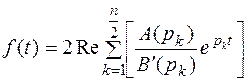 (7.5)
(7.5)
Рассмотрим примеры нахождения оригиналов.
Пример 1. Найти оригинал для изображения
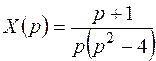 .
.
Решение.
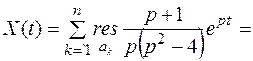
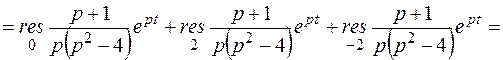
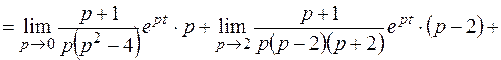
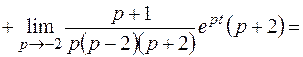
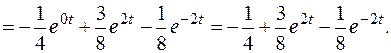
Пример 2. Найти оригинал для изображения
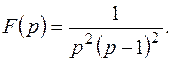
Решение.




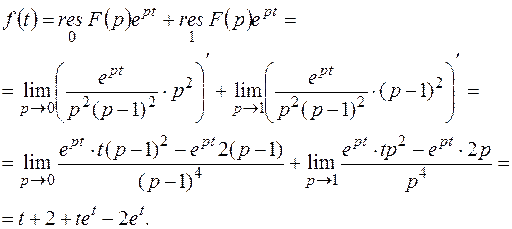
Пример 3. Найти оригинал для изображения
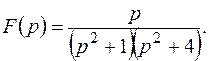
Решение. Так как изолированные особые точки 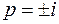 и
и 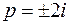 полюса второго порядка являются комплексно сопряженными, то
полюса второго порядка являются комплексно сопряженными, то
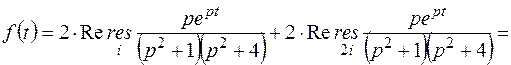
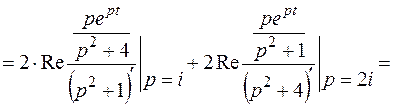

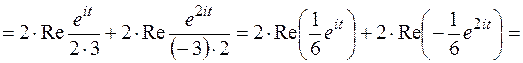
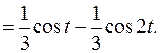
 Пример 4. Найти оригинал, если дано изображение
Пример 4. Найти оригинал, если дано изображение 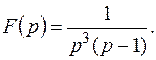
Решение.
1 способ
Преобразуем 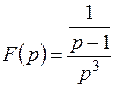 , и воспользуемся теоремой интегрирования оригинала:
, и воспользуемся теоремой интегрирования оригинала:
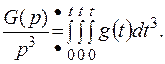
Так как 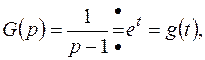 то
то
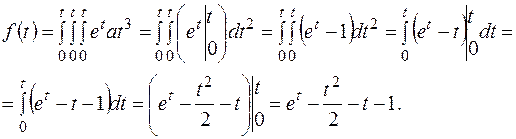
2 способ
Преобразуем 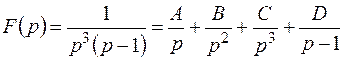
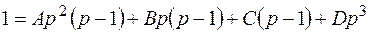 .
.
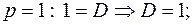
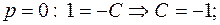
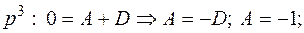
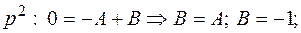
тогда  .
.
3 способ
Так как 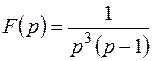 имеет две изолированные особые точки:
имеет две изолированные особые точки:  - простой полюс и
- простой полюс и 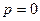 - полюс третьего порядка, то
- полюс третьего порядка, то
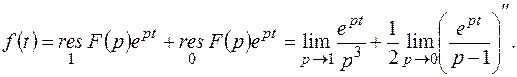
Найдем:
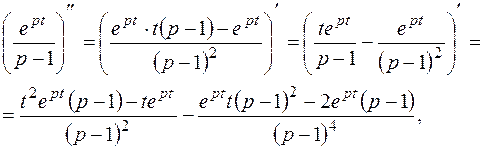

4 способ
Так как  а
а 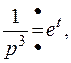 и
и 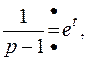 по теореме Бореля
по теореме Бореля
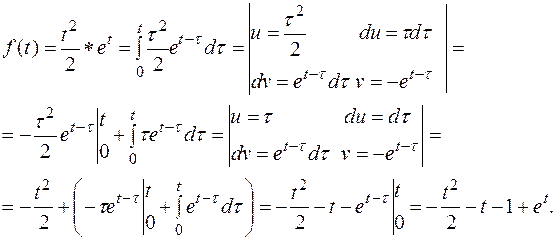
Дата добавления: 2021-11-16; просмотров: 544;











