Аффинные преобразования, их свойства

О п р е д е л е н и е. Преобразование плоскостиназывается аффинным, если оно переводит прямую в прямую и сохраняет простое отношение любых трех коллинеарных точек.

Таким образом, любое подобие, в частности, любое движение, является примером аффинного преобразования.

По аналогии с движением можно доказать теорему о задании аффинного преобразования парой соответствующих аффинных реперов:

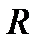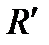Т е о р е м а. Для пары аффинных реперов и существует единственное аффинное преобразование, которое репер 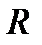переводит в репер 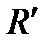. При этом аффинном преобразовании точке с заданными координатами в репере 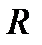соответствует точка с теми же координатами в репере .

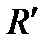Д о к а з а т е л ь с т в о. Отображение плоскости в себя, при котором каждой точке с указанными координатами в репере 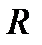соответствует точка с теми же координатами в репере 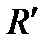, является аффинным преобразованием плоскости, переводящим репер 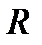в 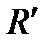(обосновать).

Далее самостоятельно покажите, что любое аффинное преобразование 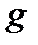, также переводящее репер 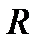в 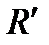, совпадает с заданным преобразованием.

С л е д с т в и е. Если аффинное преобразование имеет три неколлинеарные неподвижные точки, то это преобразование является тождественным.

Аналогично тому, как это было сделано для движений, можно вывести формулы аффинного преобразования:

.

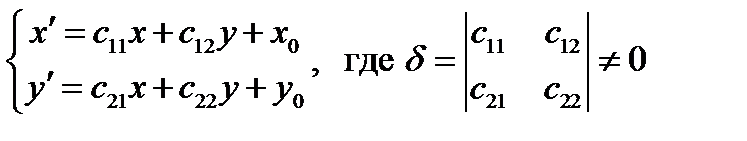Из определения аффинного преобразования и этих формул имеем свойства аффинных преобразований:

1. Аффинное преобразование репер переводит в репер.

2. Аффинное преобразование либо сохраняет, либо меняет ориентацию плоскости. Таким образом, имеем аффинные преобразования I и II рода.

3. Приаффинном преобразовании прямая переходит в прямую, параллельные прямые в параллельные прямые, отрезок в отрезок, луч в луч, угол в угол, полуплоскость в полуплоскость.