Анализ симплекс-таблиц
Математическая модель является прекрасным средством получения ответов на широкий круг вопросов, возникающих при планировании, проектировании и в ходе управления производством. Так на этапе планирования целесообразно находить варианты плана при различных вариантах номенклатуры, ресурсов, целевых функций и т.д.
При оперативном управлении решается достаточно широкий и важный круг вопросов, которые возникают при ежедневном обеспечении производственного процесса. Мы рассмотрим лишь те вопросы оперативного управления, которые могут быть решены с помощью моделей, уже составленных при планировании. «Что будет, если пять человек из числа трудовых ресурсов отвлекут на другие работы? Что будет, если сырья поставят на 20% меньше? Какую продукцию следует выпускать, если изменились цены?» Рассмотрим, как находить ответы на эти вопросы на конкретном примере.
Допустим, предприятие должно выпускать продукцию четырех видов: П1,П2,П3,П4, используя для этого три вида ресурсов. Располагаемые ресурсы, нормы расходов материалов и прибыль приведены в Таблице 5А.
ТАБЛИЦА 5А
| Элемент | Вид продукции | Располагаемый | |||
| модели | П1 | П2 | П3 | П4 | ресурс |
| Ресурсы: | |||||
| трудовые | |||||
| сырье | |||||
| оборудование | |||||
| Прибыль с единицы продукта | --- | ||||
| План | х1 | х2 | х3 | х4 | --- |
ìx1 + x2 + x3+ x4 £ 16
ï6x1 + 5x2 + 4x3+ 3x4 £ 110
(5.20) í4x1 + 6x2 + 10x3+ 13x4 £ 100
îxj ³ 0, j ³ 1,4.
F = 60x1 + 70x2 + 120x3 + 130x4 ® max
От системы неравенств (5.20) перейдем к системе уравнений. Для этого, в каждое неравенство добавим по одной дополнительной переменной: yi ³ 0, i ³ 1,m. Тогда получим систему уравнений:
ìx1 + x2 + x3+ x4 + y1 =16
ï6x1 + 5x2 + 4x3+ 3x4 + y2 =110
(5.21) í4x1 + 6x2 + 10x3+ 13x4 + y3 =100
îxj ³ 0, j = 1,4; yi ³ 0, i = 1,3.
F = 60x1 + 70x2 + 120x3 + 130x4 ® max
Затем перепишем систему (5.21) в следующем виде:
ì y1 =16 - (x1 + x2 + x3+ x4)
ï y2 =110 - (6x1 + 5x2 + 4x3+ 3x4)
(5.22) í y3 =100 - (4x1 + 6x2 + 10x3+ 13x4)
îF = 0 - (-60x1 - 70x2 - 120x3 - 130x4)
Систему (5.22) можно представить в виде Таблицы 5В, которую составляют следующим образом: свободные переменные, заключенные в скобки, выносят в верхнюю строку таблицы. В остальные столбцы записывают свободные члены и коэффициенты перед свободными переменными. Эта, так называемая симплекс таблица, служит основой для решения задач линейного программирования. В этой таблице переменные, являющиеся свободными, в данном случае x1, x2, x3, x4 по условию равны 0. Поскольку свободные переменные равны 0, то из системы (5.22) видно, что базисные переменные y1, y2, y3, а также целевая функция F, которую записывают снизу, равны свободным членам. Значит y1=16, y2=110, y3=100, F=0.
ТАБЛИЦА 5В
| Величина | Свободный | Свободные переменные | |||
| член | х1 | х2 | х3 | х4 | |
| Базисные переменные: | |||||
| y1 | |||||
| y2 | |||||
| y3 | |||||
| Индексная строка (F) | 0 | - 60 | - 70 | - 120 | - 130 |
Напомним, что в системе (5.21) общее число переменных N=n+m, где n - число основных переменных, m - число дополнительных переменных. Все переменные можно подразделить с одной стороны на основные и дополнительные, а с другой - на базисные и свободные.
þ Свободными переменными будем называть такие, которые равны 0.
Из теории известно, что n переменных в допустимом решении должны быть равны 0 , т.е. столько же переменных, сколько и основных. Однако, из этого ни в коей мере не следует, что нулю равны все основные переменные. Если из общего числа переменных N=n+m будут свободными n переменных, то очевидно, что m переменных будут базисными, т.е. не равны нулю. С учетом введенных терминов можно сказать, что целью решения задачи ЛП является нахождение базисных и свободных переменных.
Для задачи ЛП, записанной в виде симплекс таблицы, можно сформулировать признаки допустимого и оптимального решений. Решение является допустимым, если в симплекс таблице в столбце свободных членов все значения, относящиеся к базисным переменным будут неотрицательными. Оптимальное значение, как мы знаем, может либо минимизировать, либо максимизировать значение целевой функции. В связи с этим, для оптимальных значений есть два признака: один для случая минимизации целевой функции, другой - для случая максимизации.
Целевая функция имеет минимальное значение, если, во-первых, решение является допустимым, т.е. свободные члены будут неотрицательными, а во=вторых, все элементы в строке целевой функции (свободный член не рассматривается) будут неположительными. При этом целевая функция равна свободному члену. Таким образом можно сделать вывод, что в Табл. 5В получено оптимальное решение нашей задачи для случая минимизации целевой функции.
Действительно, если x1= x2= x3= x4 = 0 мы никакой продукции не выпускаем и при этом прибыль F=0. Дополнительные переменные y1, y2, y3, показывающие объем неиспользованных ресурсов, равны, соответственно: 16, 110,100, т.е. тому ресурсу, который имеется в наличии. В самом деле, мы ничего не выпускаем, но не тратим ресурсы. Следовательно, данные в Табл. 5В соответствуют такой вершине ОДР, в которой целевая функция принимает минимальное значение.
Признак максимизации целевой функции формируется следующим образом: целевая функция имеет максимальное значение, если, во-первых, решение является допустимым, а во-вторых, все элементы в строке целевой функции (свободный член не рассматривается) будут неотрицательными.
Поскольку Табл. 5В не удовлетворяет данному признаку, то необходимо перейти к другой вершине ОДР. Переход от одной вершины к другой, производится по определенному алгоритму симплекс-метода, который заключается в обмене переменных.
þ Каждый переход от одной вершины к другой, который называется итерацией, состоит в том, что одна базисная переменная приравнивается к нулю, т.е. переходит в свободную, а одна свободная переменная переводится в базисную.
На каждой итерации проверяют удовлетворение признаков допустимого и оптимального решений. Такая процедура продолжается до тех пор, пока не будут удовлетворены оба признака. Применительно к нашей задаче переходим к следующей симплекс-таблице, полученной после первой итерации.
Переход к новой таблице осуществляем следующим способом: в индексной строке, где находится целевая функция находим наибольшее по абсолютному значению отрицательное число. Найденное число определяет ведущий столбец. Затем мы делим свободные члены на положительные элементы ведущего столбца и выбираем из полученных отношений наименьшее. Наименьшее отношение определяет ведущую строку. В нашем случае имеем:
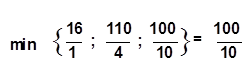
Таким образом, ведущим столбцом будет столбец х3, а ведущей строкой будет строка y3. На пересечении ведущего столбца и ведущей строки будет разрешающий элемент. В нашем случае это число 10. Таким образом, ведущей строкой будет строка y3, обозначим ее через Ar. Ведущим столбцом будет столбец х4, обозначим его через Ak, и, следовательно, разрешающий элемент Ark = 10.
Теперь приступаем к составлению второй таблицы. В этой таблице элементы направляющей строки равны этому элементу ведущей строки, деленному на разрешающий элемент, и находятся в соотношении:
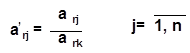
Элементы любой другой строки j находят из соотношения:
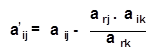
Т.е. чтобы получить любой другой элемент новой симплексной таблицы, нужно от соответствующего элемента прежней таблицы отнять произведение элемента ведущей строки на элемент ведущего столбца, разделенное на разрешающий элемент.
После этих преобразований новая симплексная таблица после первой итерации примет вид Таблицы 5С.
ТАБЛИЦА 5С
| Величина | Свободный | Свободные переменные | |||
| член | х1 | х2 | х3 | х4 | |
| Базисные переменные: | |||||
| y1 | 0,6 | 0,4 | - 0,3 | ||
| y2 | 4,4 | 2,6 | - 2,2 | ||
| y3 | 0,4 | 0,6 | 1,3 | ||
| Индексная строка (F) | 1200 | - 12 | 2 | 0 | 26 |
В Табл. 5С в индексной строке только один отрицательный элемент, следовательно, ведущим столбцом будет х1, а ведущую строку определяем по наименьшему отношению:
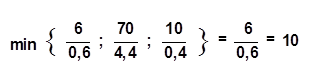
Т. о. Ведущей строкой будет y1, а разрешающим элементом число 0,6.
Применительно к нашей задаче последняя симплекс-таблица, полученная после второй итерации, будет иметь вид:
ТАБЛИЦА 5D
| Величина | Свободный | Свободные переменные | |||
| член | х1 | х2 | х3 | х4 | |
| Базисные переменные: | |||||
| х1 | 5/3 | 2/3 | - 1/6 | - 1/2 | |
| y2 | -22/3 | - 1/3 | 1/3 | ||
| х3 | - 2/3 | 1/3 | 1/6 | 3/2 | |
| Индексная строка (F) | 1320 | 20 | 10 | 10 | 20 |
Из этой таблицы видно, что в столбце свободных членов все элементы положительные. Значит решение является допустимым. В строке целевой функции все элементы тоже положительные. Следовательно, это решение оптимальное и максимизирует целевую функцию. При этом оптимальным планом будут следующие величины: х1*=10, х3*=6 (значит, они - базисные) и х2*=х4*=0 (т.к. они свободные). При этом целевая функция F=1320.
Вот результат решения задачи. Однако, с помощью симплекс-таблицы можно узнать еще много полезных сведений. Так их этой же таблицы видим, что свободные переменные y1=y3=0, а базисная переменная y2=26. А это значит, что в оптимальном плане резервы трудовых ресурсов и оборудования равны нулю. Иными словами, эти ресурсы используются полностью. Вместе с тем резерв ресурсов сырья y2=26, что свидетельствует о том, что имеются излишки сырья. Вот какие полезные сведения можно получить из окончательной симплекс-таблицы.
Дата добавления: 2021-09-25; просмотров: 605;











