Зависимость между случайными величинами

При изучении процессов функционирования сложных систем приходится иметь дело с целым рядом одновременно действующих случайных величин. Для уяснения механизма явлений, причинно-следственных связей между элементами системы и т.д., по полученным наблюдениям мы пытаемся установить взаимоотношения этих величин.

В математическом анализе зависимость, например, между двумя величинами выражается понятием функции y=f(x), где каждому значению одной переменной соответствует только одно значение другой. Такая зависимость носит название функциональной.

Гораздо сложнее обстоит дело с понятием зависимости случайных величин. Как правило, между случайными величинами (случайными факторами), определяющими процесс функционирования сложных систем, обычно существует такая связь, при которой с изменением одной величины меняется распределение другой. Такая связь называется стохастической, или вероятностной. При этом величину изменения случайного фактора Y, соответствующую изменению величины Х, можно разбить на два компонента. Первый связан с зависимостью Y от X, а второй с влиянием "собственных" случайных составляющих величин Y и X. Если первый компонент отсутствует, то случайные величины Y и X являются независимыми. Если отсутствует второй компонент, то Y и X зависят функционально. При наличии обоих компонент соотношение между ними определяет силу или тесноту связи между случайными величинами Y и X.

Существуют различные показатели, которые характеризуют те или иные стороны стохастической связи. Так, линейную зависимость между случайными величинами X и Y определяет коэффициент корреляции.

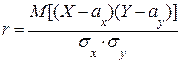,(3.1)

где 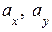– математические ожидания случайных величин X и Y.

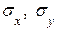– средние квадратические отклонения случайных величин X и Y.

Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону. Если случайные величины X и Y связаны строгой линейной функциональной зависимостью, например,

y=b₀+b₁x₁,

то коэффициент корреляции будет равен 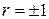; причем знак соответствует знаку коэффициента b₁ .Если величины X и Y связаны произвольной стохастической зависимостью, то коэффициент корреляции будет изменяться в пределах

.

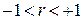Следует подчеркнуть, что для независимых случайных величин коэффициент корреляции равен нулю. Однако коэффициент корреляции как показатель зависимости между случайными величинами обладает серьезными недостатками. Во-первых, из равенства r = 0 не следует независимость случайных величин X и Y (за исключением случайных величин, подчиненных нормальному закону распределения, для которых r = 0 означает одновременно и отсутствие всякой зависимости). Во- вторых, крайние значения 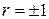также не очень полезны, так как соответствуют не всякой функциональной зависимости, а только строго линейной.

Полное описание зависимости Y от X , и притом выраженное в точных функциональных соотношениях, можно получить, зная условную функцию распределения .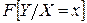

Следует отметить, что при этом одна из наблюдаемых переменных величин считается неслучайной. Фиксируя одновременно значения двух случайных величин X и Y, мы при сопоставлении их значений можем отнести все ошибки лишь к величине Y. Таким образом, ошибка наблюдения 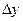будет складываться из собственной случайной ошибки величины Y и из ошибки сопоставления, возникающей из-за того, что с величиной Y сопоставляется не совсем то значение X, которое имело место на самом деле.

Однако отыскание условной функции распределения, как правило, оказывается весьма сложной задачей. Наиболее просто исследовать зависимость между Х и Y при нормальном распределении Y, так как оно полностью определяется математическим ожиданием и дисперсией. В этом случае для описания зависимости Y от X не нужно строить условную функцию распределения, а достаточно лишь указать, как при изменении параметра X изменяются математическое ожидание и дисперсия величины Y.

Таким образом, мы приходим к необходимости отыскания только двух функций:

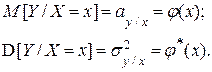(3.2)

Зависимость условной дисперсии D [Y/X=x] от параметра Х носит название сходастической зависимости. Она характеризует изменение точности методики наблюдений при изменении параметра и используется достаточно редко.

Зависимость условного математического ожидания M[Y/x=x] от X носит название регрессии, она дает истинную зависимость величин Х и У, лишенную всех случайных наслоений. Поэтому идеальной целью всяких исследований зависимых величин является отыскание уравнения регрессии, а дисперсия используется лишь для оценки точности полученного результата.